Общая характеристика и некоторые определения

Любая связная структура может быть представлена ориентированным графом, в любой узел которого может входить любое количество связок, исходящих из других узлов. Такие структуры называются в общем случае сетевыми (графовыми) структурами или сетями. Древовидные структуры или просто деревья являются частными случаями сетевых. Элементы структуры в соответствии с терминологией теории графов называют узлами (node).

Деревом (tree) называется сетевая структура данных, которая характеризуется следующими свойствами:

1) существует единственный элемент (узел), на который не ссылается никакой другой элемент и который называется корнем (root);

2) начиная с корня и следуя по определенной цепочке структурных указателей, задающих непосредственных предшественников и последователей, можно осуществить доступ к любому узлу дерева;

3) на каждый элемент дерева, кроме корня, имеется единственный структурный указатель от другого элемента.

Определенная таким образом структура называется корневым деревом (sink tree). На рисунке 9.1 представлен древовидный граф, отражающий отношения между элементами, информационные поля которых содержат символы-метки А, В, ..., Н. Как видно из этого рисунка, деревья принято рисовать перевернутыми (т. е. «растущими сверху вниз»), при этом корень оказывается самым верхним узлом.

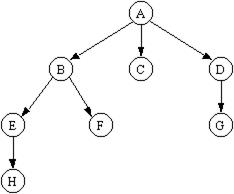
Рисунок 9.1 – Логическая структура дерева

Линию связи между парой узлов дерева называют ветвью (branch), а сами узлы - вершинами (vertex). Те узлы, которые не ссылаются ни на какие другие узлы дерева, называются листьями (leaf) или концевыми (end vertex), висячими (dangling vertex) вершинами. Узел, не являющийся листом или корнем, называется узлом ветвления или промежуточным (внутренним) узлом.

Если в дереве вершина Х ссылается на вершину Y, то Х называют родителем (parent node) вершины Y, а Y - сыном или дочерней вершиной (child node) вершины Х. Если же вершина Х ссылается на узлы Y₁, Y₂, ... , Y_n, то последние называются сыновьями вершины Х. Все вершины, имеющие общего родителя, называются братьями. Очевидно, любая ветвь дерева устанавливает между двумя вершинами отношение «родитель - сын».

В дереве обычно задается порядок старшинства братьев: самый левый на графе из братьев считается старшим братом (старшим сыном общего родителя); порядок старшинства убывает слева направо. Как правило, старшинство братьев задается с помощью переменной, называемой индексом старшинства, например, Y₁ - самый старший из братьев (индекс равен 1), Y_n - самый младший брат. Если в дереве задан порядок старшинства братьев, то такое дерево называется упорядоченным. Если порядок старшинства игнорируется, то дерево называется неупорядоченным. На рисунке 9.2 изображены различные упорядоченные деревья.

Рисунок 9.2 – Два различных упорядоченных дерева

Число сыновей у родителя Х называется степенью исхода (или просто степенью) вершины Х. Максимальная степень всех вершин называется степеньюдерева. Дерево называется m-арным, если его степень равна m. Если степень исхода каждой вершины одного и того же дерева равна либо m, либо нулю, то такое m‑арное дерево называется полным; в противном случае дерево является неполным m-арным деревом. Изображенное на рисунке 9.1 дерево имеет степень 3; оно является неполным троичным (3-арным) деревом. Дерево степени 2 называется бинарным или двоичным деревом.

Все вершины, которые встречаются на пути от корня до вершины Х, называются предками вершины Х. С другой стороны, все вершины, для которых вершина Y является предком, называются потомками вершины Y. Родитель вершины Х называется непосредственнымпредком для Х; вершина-сын называется непосредственным потомком. Таким образом, дерево можно определить как корень со всеми его потомками.

Путем от вершины Х к вершине Y называется последовательность вершин, которые встречаются при перемещении по ветвям от Х к Y. Количество ветвей, которые нужно пройти по пути от вершины Х к вершине Y называется длиной этого пути. Длина пути от корня до некоторого узла Х называется уровнем яруса или, просто, уровнем узла Х. (Уровень узла дерева иногда называют глубиной этого узла). Уровень корня равен нулю, уровень узла Е на рисунке 9.1 равен 2. Сумма длин путей для всех элементов называется длиной внутреннего пути.

Высотой узла Х называется длина самого длинного пути от Х до какого‑ либо листа. Например, высота вершины В на рисунке 9.1 равна 2, а высота вершины D равна 1. Высота дерева совпадает с высотой его корня.

Деревья, использующие указатели для связи вершин, являются ориентированными. Структура дерева такова, что каждая его внутренняя вершина является корнем древовидной структуры, называемой поддеревом (subtree) исходного дерева. Действительно, если в некотором дереве убрать его корень и ветви, соединяющие его с вершинами первого уровня, то получим набор поддеревьев, корни которого - это вершины первого яруса исходного дерева. Множество несвязанных между собой деревьев называется лесом (forest).

Если развернуть логическую структуру односвязного списка (см. рисунок 6.1) на 90 градусов так, чтобы начальный элемент оказался наверху, то получим дерево, в котором каждая вершина имеет не более одного поддерева. Такое дерево (оно имеет степень 1) называется вырожденным деревом.