Бинарное дерево

9.4.1 Структура бинарного дерева

Упорядоченные деревья второй степени (m-арные деревья при m=2) называют двоичнымиилибинарнымидеревьями. Упорядоченное бинарное дерево можно определить как множество вершин, которое либо пусто, либо состоит из корня с двумя отдельными двоичными деревьями, которые называют левымиправымподдеревьямиэтого корня. Деревья степени больше двух называют сильно ветвящимися деревьями (multiway trees).

При представлении бинарного дерева в виде связного списка каждый элемент может содержать поля данных и два структурных указателя: указатель (Left) левого сына и указатель (Right) правого сына. Такое представление называется естественным представлением бинарного дерева.

Тип бинарного дерева (базовый тип дерева) может быть объявлен следующим образом:

Type

Pvertex = ^Tvertex;

Tvertex = Record

Dat: <поля данных>;

Left, Right: Pvertex;

End;

Var CurrentVertex, Root: Pvertex;

CountVertex: Integer;

где Dat, как и ранее, - совокупность информационных полей; Left и Right поля структурных указателей. Поля данных мы будем использовать для размещения меток вершин. Переменные-указатели CurrentVertex и Root и необходимы для идентификации соответственно некоторой текущей вершины и корня. CountVertex - количество вершин в дереве.

На рисунке 9.8 изображена структура естественного представления бинарного дерева (пустые поля указателей содержат пустые ссылки).

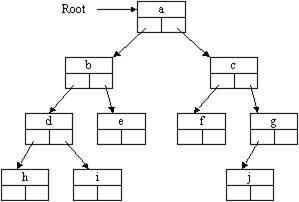
Рисунок 9.8 - Естественное представление бинарного дерева

9.4.2 Формирование бинарного дерева

Предположим, что нужно построить такое бинарное дерево, которое при заданном количестве вершин N имела бы минимальную высоту. Очевидно, минимальная высота дерева достигается, если на всех уровнях, кроме последнего, поместить максимально возможное число вершин. Этого можно добиться, размещая «приходящие» в дерево вершины поровну слева и справа от той вершины, которая будет для них родителем. В результате при каждом увеличении количества вершин мы будем получать деревья, показанные на рисунке 9.9.

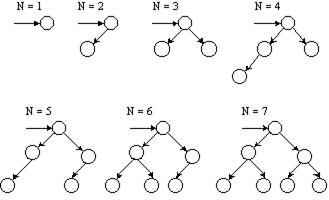
Рисунок 9.9 - Сбалансированные бинарные деревья для различных N

Дерево, имеющее структуру, показанную на рисунке 9.9, называется сбалансированным деревом (balanced tree, AVL-tree). В таком дереве число потомков в левом и правом поддереве любой вершины отличается не более, чем на 1.

Алгоритм формирования сбалансированного бинарного дерева допускает следующую рекурсивную формулировку:

- взять одну вершину в качестве корня;

- построить тем же способом левое поддерево с Nleft = N Div 2 вершинами;

- построить тем же способом правое поддерево с Nright = N - Nleft - 1 вершинами.

Вышеприведенному алгоритму соответствует рекурсивная функция BinaryTreeCreate, приведенная ниже:

Function BinaryTreeCreate(N: Integer): Pvertex;

Var Nleft, Nright: Integer;

Begin

If N = 0 Then Tree:= Nil