Else Begin. BinaryTreeCreate:= CurrentVertex;

Nleft:= N Div 2;

Nright:= N - Nleft - 1;

New(CurrentVertex);

BinaryTreeCreate:= CurrentVertex;

With CurrentVertex^ Do Begin

<занесение данных в поля Dat>

Left:= BinaryTreeCreate(Nleft);

Right:= BinaryTreeCreate(Nright);

End;

End;

End;

Для использования функции BinaryTreeCreate нужно передать ей значение числа вершин и выполнить вызов в следующей форме:

Root:= BinaryTreeCreate(CountVertex);

9.4.3 Обход бинарного дерева

Методы обхода дерева любой степени, рассматриваемые в подразделе 10.3, переформулируем в отношении бинарных деревьев.

1) Нисходящий обход:

- обработка корня,

- нисходящий обход левого поддерева,

- нисходящий обход правого поддерева.

Вершины дерева, изображенного на рисунке 9.8, поступали бы на обработку при обходе нисходящим методом в следующем порядке: a, b, d, h, i, e, c, f, g, j.

2) Смешанный обход:

- смешанный обход левого поддерева,

- обработка корня,

- смешанный обход правого поддерева.

Например, при обходе дерева на рисунке 9.8 смешанным методом вершины обрабатываются в следующей последовательности: h, d, i, b, e, a, f, c, j, g.

3) Восходящий обход:

- восходящий обход левого поддерева,

- восходящий обход правого поддерева,

- обработка корня.

Порядок обработки вершин того же дерева при восходящем обходе выглядит так: h, i, d, e, b, f, j, g, c, a.

Для методов обхода в применении к бинарным деревьям часто применяют специфичные названия: нисходящий обход называют обходом pre‑order, смешанный обход - обходом in-order и восходящий - обходом post‑order. Обход post‑order чаще всего применяется для уничтожения всех вершин в бинарном дереве, когда процесс уничтожения можно было бы описать следующим образом: «чтобы уничтожить все вершины бинарного дерева, необходимо уничтожить левое поддерево корня, затем правое поддерево, а затем и сам корень».

Все три метода легко представить рекурсивными процедурами. Прежде чем это сделать, необходимо определить процедуру, активируемую на этапе «обработка». Такая процедура должна выполнять некоторые действия над вершиной, к которой получен доступ на текущем шаге просмотра. А доступ к элементу связной структуры легче всего обеспечить через указатель, который назовем pNode. Текст такой процедуры может выглядеть, например, следующим образом:

Procedure ProcessingNode(pNode: Pvertex);

Var S: String;

Begin

S:= <преобразование информационных
полей элемента рNode^ в строку>;

Form1.Memo1.Lines.Append(S);

End;

Теперь можно привести тексты трех подпрограмм обхода, которые реализуют приведенные выше рекурсивные алгоритмы:

ProcedurePreOrder(pRoot: Pvertex);

Begin

If (aRoot <> Nil) Then Begin

ProcessingNode(pRoot);

PreOrder(pRoot^.Left);

PreOrder(pRoot^.Right);

End;

End;

ProcedureInOrder(pRoot: Pvertex);

Begin

If (aRoot <> Nil) Then Begin

InOrder(pRoot^.Left);

ProcessingNode(pRoot);

InOrder(pRoot^.Right);

End;

End;

ProcedurePostOrder(pRoot: Pvertex);

Begin

If (aRoot <> Nil) Then Begin

PostOrder(pRoot^.Left);

PostOrder(pRoot^.Right);

ProcessingNode(pRoot);

End;

End;

Для активации любой из этих трех процедур, следует воспользоваться вызовом в следующем виде:

<имя процедуры>(Root);

где Root - указатель корня, например: PostOrder(Root).

9.4.4 Преобразование любого дерева к бинарному дереву

Любое m-арное дерево (т. е. дерево степени m) может быть преобразовано в эквивалентное ему бинарное дерево, которое проще исходного дерева с точки зрения представления в памяти и обработки. Графически такое преобразование сводится к следующим действиям:

1) сначала в каждом узле исходного дерева вычеркиваем все ветви, кроме самой левой ветви, которая соответствует ссылке на старшего сына;

2) в получившемся графе соединяем те узлы одного уровня, которые являются братьями в исходном дереве.

На рисунке 9.10 приведен пример такого преобразования, причем после него из некоторых элементов, исходят две ссылки: горизонтальная соединяет данный элемент с его младшим (в исходном дереве) братом, а вертикальная - с его старшим сыном. Если на рисунке 9.10 повернуть все ссылки на 45° по часовой стрелке, то получим структуру, очень похожую на двоичное дерево. Однако считать ее таковым было бы ошибкой, поскольку функционально горизонтальные и вертикальные ссылки на рисунке 9.10 б имеют совершенно разный смысл. Правильнее было бы использовать следующую интерпретацию: после выполнения указанных преобразований из сыновей каждого родителя образуется линейный список, причем на старшего сына указывает ссылка от его родителя, а сам старший сын находится в голове списка своих братьев.

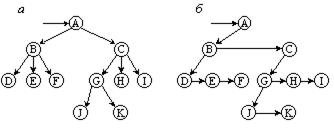
Рисунок 9.10 - Преобразование 3-арного дерева к бинарному

Пользуясь аналогичным алгоритмом можно представить в виде двоичного дерева и лес. На рисунке 9.11 показаны этапы преобразования леса из двух деревьев в бинарное дерево.

Переход от m-арного дерева (или леса) к представлению в виде двоичного дерева при естественном связном хранении сокращает объем занимаемой памяти, поскольку каждый элемент m-арного дерева должен иметь m полей для логических указателей, тогда как элемент двоичного дерева имеет только два таких поля. С другой стороны, при таком преобразовании нужно помнить о функциональном назначении левой и правой ссылок и учитывать это при обработке дерева.

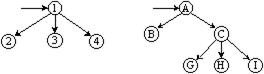
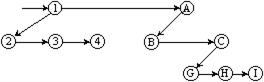
Рисунок 9.11 - Преобразование леса к бинарному дереву