Else Begin

a[k]:= a[j]; k:= k+h; j:=j-1; r:=r-1

End

End;

{копирование остатка серии из j}

While r<>0 Do Begin

a[k]:= a[j]; k:= k+h; j:= j-1; r:= r -1

End;

{копирование остатка серии из i}

While q<>0 Do Begin

a[k]:= a[i]; k:= k+h; i:= i+1; q:= q-l

End;

h:= -h; t:= k; k:= l; l:=t

Until m=0;

up:= -up; p:=2*p;

Until p>=n

If -up Then For i:=1 To N Do a[i]:=a[i+N];

End; {Mergesort}

Алгоритм сортировки прямым слиянием выдерживает сравнение даже с усовершенствованными методами внутренней сортировки. Но затраты на управление индексами довольно высоки, кроме того, существенным недостатком является использование памяти размером 2N элементов. Поэтому сортировка слиянием редко применяется при работе с массивами, т. е. данными, расположенными в оперативной памяти.

11.3.2 Сортировка естественным слиянием

В случае простого слияния мы ничего не выигрываем, если данные уже частично рассортированы. На k-м проходе длина всех сливаемых последовательностей меньше или равна 2^k. При этом не учитывается то, что более длинные последовательности могут быть уже упорядочены и, следовательно, их можно сливать. Фактически можно было бы сразу сливать какие-либо упорядоченные подпоследовательности длиной m и k в одну последовательность из m+k элементов. Метод сортировки, при котором каждый раз сливаются две самые длинные возможные подпоследовательности, называется естественным слиянием.

Упорядоченную подпоследовательность часто называют цепочкой. Но, поскольку слово «цепочка» чаще используется для обозначения односвязного списка, мы будем использовать слово серия, когда речь идет об упорядоченной подпоследовательности. Сортировка естественным слиянием сливает последовательности не фиксированной длины, а серии. Серии имеют то свойство, что при слиянии двух последовательностей, каждая из которых содержит n серий, возникает одна последовательность, содержащая ровно n/2 серий. Таким образом, на каждом проходе общее число серий уменьшается вдвое, и число необходимых пересылок элементов в худшем случае равно N×log₂N, а в обычном случае даже меньше. Ожидаемое число сравнений, однако, намного больше, так как кроме сравнений, необходимых для упорядочения элементов, требуются еще сравнения соседних элементов каждого файла для определения концов серии.

Пусть исходная последовательность элементов задана в виде файла а, который в конце работы должен содержать результат сортировки. Используются две вспомогательные ленты b и с. Каждый проход состоит из фазы распределения, которая распределяет серии поровну из а в b и с, и фазы слияния, которая сливает серии из b и с в а. В качестве примера ниже показан файл а в исходном состоянии (строка 1) и после каждого прохода (строки 2 - 4). В естественном слиянии участвуют 20 чисел. Заметим, что требуются только три прохода. Сортировка заканчивается, как только число серий в а будет равно 1. (Предполагается, что в исходном файле имеется хотя бы одна непустая серия.)

17, 31, | 05, 59, | 13, 41, 43, 67, | 11, 23, 29, 47, | 03,07, 71, | 02, 19, 57, | 37, 61

05, 17,31, 59, | 11, 13, 23, 29, 41, 43, 47, 67, | 02,03, 07,19,57,71, | 37, 61

05,11,13,17,23,29,31,41,43,47,59,67, | 02, 03, 07, 19, 37, 57, 61, 71

02, 03, 05, 07, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 57, 59, 61, 67, 71

Схематично процесс сортировки естественным слиянием можно отобразить рисунком 11.7.

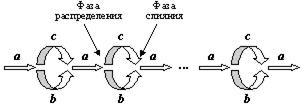
Рисунок 11.7 - Фазы сортировки естественным слиянием

При просмотре последовательности, выполняемом на фазе разделения (распределения) определяется конец очередной серии. Элемент, расположенный на конце предыдущей серии должен быть больше первого элемента следующей серии, т. е. нужно сравнивать ключи двух последовательных элементов. Однако природа последовательности такова, что непосредственно доступен только один-единственный элемент. Поэтому невозможно избежать «заглядывания вперед», т. е. необходимо считывать в некий «буфер» первый еще не считанный элемент последовательности.

Процесс сравнения и выбора ключей при слиянии заканчивается, как только исчерпана одна из двух серий. После этого оставшаяся неисчерпанной серия должна быть просто передана в результирующую серию, т.е. скопирована в ее «хвост».

11.3.3 Сортировка многопутевым слиянием

Затраты на любую последовательную сортировку пропорциональны числу требуемых проходов, так как по определению при каждом из проходов копируются все данные. Один из способов сократить это число – распределять серии в более чем две последовательности (ленты).

Допустим, исходная последовательность хранится на ленте а. Кроме того, используются r дополнительных лент: b₁, b₂ , …, b_r. Тогда r-путевое слияние выполняется следующим образом: первая серия на ленте а распределяется на ленту b₁, вторая - на ленту b₂ и т. д., r-ая серия - на ленту b_r; затем (r+1)-ая серия на ленту b₁, (r+2)-ая - на ленту b₂ и так до тех пор, пока не распределится последняя из серий ленты а. Затем начальные серии всех дополнительных лент, сливаются на ленту а в одну общую серию, вторые серии дополнительных лент сливаются во вторую серию на ленту а и т. д. Подобный процесс может быть представлен схемой, показанной на рисунке 11.8.

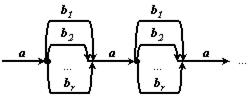
Рисунок 11.8 - Схема r-путевого слияния

Таким образом, естественное слияния является 2‑х путевым слиянием.

Слияние p серий поровну распределенных в rпоследовательностей (лент) даст в результате p/rсерий. Второй проход уменьшит это число до р/r², третий – до р/r³ и т. д., после k проходов останется r/p^kсерий. Поэтому общее число проходов, необходимых для сортировки N элементов с помощью r-путевого слияния, равно k=log_rN. Поскольку в каждом проходе выполняется Nопераций копирования, то в самом плохом случае понадобится N×log_rNтаких операций.

На практике многопутевое слияние реализуется как сбалансированное многопутевое слияние с одной единственной фазой, которое предполагает, что в каждом проходе участвует равное количество входных и выходных файлов (лент), в которые по очереди распределяются последовательные серии. Такой алгоритм использует rлент (r- четное число), поэтому он базируется на (r/2)-путевом слиянии. Фазы разделения и слияния как бы объединяются в одну фазу, в ходе которой серии из r/2 лент, называемых входными, не сливаются в одну общую последовательность, а тут же разделяются на другие r/2 лент (они называются выходными), после чего входные и выходные последовательности меняются местами.

11.3.4 Многофазная сортировка

В основе усовершенствований, реализованных в многофазной сортировке (Polyphase Sort), лежит отказ от жесткого понятия прохода и переход к более изощренному использованию последовательностей, называемых лентами. Этот метод был изобретен Р. Гилстэдом.

Продемонстрируем многофазную сортировку на примере с тремя последовательностями (лентами) f1, f2 и f3. В каждый момент сливаются элементы из двух лент-источников и записываются в третью ленту. Как только одна из входных последовательностей исчерпывается, она сразу же становится выходной для операции слияния из оставшейся, неисчерпанной входной последовательности и предыдущей выходной.

Поскольку известно, что p серий на каждом из входов трансформируются в pсерий на выходе, то нужно только держать список из числа серий в каждой последовательности (а не определять их действительные ключи). Будем считать, что в начале две входные последовательности f1и f2 содержат соответственно 13 и 8 серий. Следовательно, на первом проходе 8 серий из f1и f2 сливаются в f3, на втором – 5 серий из f1и f3 и сливаются в f2 и т. д. В конце концов, в f1оказывается отсортированная последовательность. Этот процесс показан на рисунке 11.9.

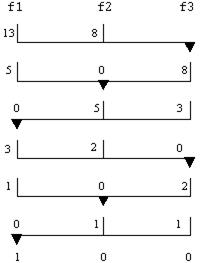
Рисунок 11.9 - Многофазная сортировка слиянием 21 серии на трех лентах

Многофазная сортировка более эффективна, чем сбалансированная многопутевая, поскольку она имеет дело с (r-1)-путевым слиянием, а не с (r/2)-путевым слиянием, если она начинается с r последовательностей (лент). Ведь число необходимых проходов приблизительно равно log_rN , где N – число сортируемых элементов, а r – степень операции слияния, – это и определяет значительное преимущество многофазной сортировки.