Разрешение коллизий при хешировании

Посмотрим, что произойдет, если мы попытаемся ввести в таблицу на рисунке 12.1 некоторую новую запись с ключом 0596993. Используя хеш-функцию КeyMod 1000, мы найдем, что h(0596993) = 993, и что запись для этого ключа должна находиться в позиции 993 в массиве. Однако позиция 993 уже занята, поскольку там находится запись с ключом 0047993. Следовательно, запись с ключом 0596993 должна быть вставлена в таблицу в другом месте.

12.3.1 Разрешение коллизий методом открытой адресации

Самым простым методом разрешения коллизий при хешировании является помещение данной записи в следующую свободную позицию в массиве. Например, на рисунке 12.1 запись с ключом 0596993 помещается в ячейку 994, которая пока свободна, поскольку 993 уже занята. Когда эта запись будет вставлена, другая запись, которая хешируется в позицию 993 (с таким ключом, как 8764993) или в позицию 994 (с таким ключом, как 2194994), вставляется в следующую свободную позицию, индекс которой в данном случае равна 995.

Этот метод называется линейным зондированием илилинейнымопробованием (linear probing); он является частным случаем некоторого общего метода разрешения коллизий при хешировании, который называется повторнымхешированием или схемой соткрытойадресацией (open-addressing schemes).

В общем случаефункцияповторногохеширования rh воспринимает один индекс в массиве и выдает другой индекс. Если ячейка массива с индексом i = h(Кey) уже занята некоторой записью с другим ключом, то функция rh применяется к значению i для того, чтобы найти другую ячейку, куда может быть помещена эта запись. Если ячейка с индексом

j = rh(i) = rh(h(key)) (12.2)

также занята, то хеширование выполняется еще раз и проверяется ячейка rh(rh(h(key))). Этот процесс продолжается до тех пор, пока не будет найдена пустая ячейка.

В нашем примере хеш-функция есть h(key)= Кey Mod 1000, а функция повторного хеширования rh(i)= (i+1) Mod 1000, т. е. повторное хеширование какого-либо индекса есть следующая последовательная позиция в данном массиве, за исключением того случая, что повторное хеширование 999 дает 0.

Поиск в такой таблице выполняется по аналогичному алгоритму:

1) аргумент поиска ArgSearch хешируется в индекс i = h(ArgSearch);

2) проверяется i-ая позиция таблицы:

- если ArgSearch совпадает с ключом i-ой записи, то поиск результативен (искомая запись имеет индекс i), поиск завершается,

- если совпадения не произошло, то переход к п. 3,

- или i-ая позиция пуста, поиск безрезультатен, поиск завершен;

3) выполняется повторное хеширование, т. е. проверяется позиция с индексом

j = rh(i) = rh(h(ArgSearch)),

и результат проверки анализируется так же, как в п. 2.

Рассмотрим данный алгоритм более подробно, чтобы понять, можно ли определить свойства некоторой «хорошей» функции повторного хеширования. Сфокусируем наше внимание на количестве повторных хеширований, поскольку это количество определяет эффективность поиска. Выход из цикла повторных хеширований может быть в одном из двух случаев. Или переменная i принимает такое значение, что ключ с индексом rh(i) равен Кey (и в этом случае найдена запись), или переменная iпринимает такое значение, что элемент с индексом rh(i) пуст; в этом случае найдена пустая позиция, и запись может быть вставлена.

Может случиться, однако, что данный цикл будет выполняться бесконечно. Для этого существуют две возможные причины. Во-первых, таблица может быть полной, так что вставить какие-либо новые записи невозможно. Эта ситуация может быть обнаружена при помощи счетчика числа записей в таблице. Когда этот счетчик равен размеру таблицы, не надо проверять дополнительные позиции.

Возможно, однако, что данный алгоритм приведет к бесконечному зацикливанию, даже если имеются некоторые пустые позиции (или даже много таких позиций). Предположим, например, что в качестве функции повторного хеширования используется функция rh(i) = (i+2) Mod 1000. Тогда любой ключ, который хешируется в нечетное целое число, повторно хешируется в следующие за ним нечетные целые числа, а любой ключ, который хешируется в четное число, повторно хешируется в следующие за ним четные целые числа. Рассмотрим ситуацию, при которой все нечетные позиции в таблице заняты, а все четные свободны. Несмотря на тот факт, что половина позиций в массиве свободна, невозможно вставить новую запись, чей ключ хешируется в нечетное число. Конечно, маловероятно, что заняты все нечетные позиции, а ни одна из четных позиций не занята. Но если использовать функцию повторного хеширования

rh(i) = (i+200)× Mod 1000,

то каждый ключ может быть помещен только в одну из пяти позиций (поскольку х× Mod 1000 = (х+1000)× Mod 1000. При этом вполне возможно, что эти пять позиций будут заняты, а большая часть таблицы будет пустой.

Свойство хорошей функции повторного хеширования состоит в том, что для любого индекса i последовательно выполняемые повторные хеширования rh(i), rh(rh(i)), ... располагаются на максимально возможное число целых чисел от 0 до N-1 (где N является числом элементов в таблице), причем в идеале - на все эти числа. Функция повторного хеширования rh(i)= (i+1)× Mod N обладает этим свойством. И действительно, любая функция rh(i)= (i+с)×Mod N, где c - некоторая константа такая, что значения с и N являются взаимно простыми числами (т. е. они одновременно не могут делиться нацело ни на какое число, кроме 1), выдает последовательные значения, которые распространяются на всю таблицу.

Имеется другая мера пригодности функции хеширования. Рассмотрим функцию повторного хеширования rh(i)= (i+1) Mod N. Предполагаем, что функция хеширования h(Key) выдает индексы, которые равномерно распределены в интервале от 0 до N-1, т.е. вероятность того, что функция h(Key) будет равна какому-либо конкретному числу в этом диапазоне, одинакова для всех чисел. Тогда первоначально, когда весь массив пуст, равновероятно, что некоторая произвольная запись будет помещена в любую заданную пустую позицию в массиве. Однако, когда записи будут вставлены и будет разрешено несколько коллизий при хешировании, это уже не будет справедливо. После большого количества вставок и разрешений коллизий с помощью повторного хеширования может возникнуть следующая ситуация: при вставке записи, у которой ключ хешируется в индекс i, обнаруживается, что i-ая позиция занята записью, ключ которой хешируется в другой индекс.

Явление, при котором два ключа, которые хешируются в разные значения, конкурируют друг с другом при повторных хешированиях, называется скучиванием или скоплекнием. При скучивании в таблице образуются локальные участки, в которых располагаются конкурирующие друг с другом записи, тогда как другие части таблицы оказываются незанятыми. Эти участки называются кластерами.

Одним способом ослабления эффекта скучивания является использованиедвойногохеширования, которое состоит в использовании двух хеш-функций - h1(key) и h2(key). Функция h1, которая называетсяпервичной хеш-функцией, используется первой при определении той позиции, в которую должна быть помещена запись. Если эта позиция занята, то последовательно используется функция повторного хеширования

rh(i) = (i+h2(key)) Mod N

до тех пор, пока не будет найдена пустая позиция. Записи с ключами key1 и key2 не будут соревноваться за одну и ту же позицию, если h2(key1) не равноh2(key2). Это справедливо, несмотря на ту возможность, чтоh1(key1) может в действительности равняться h1(key2). Функция повторного хеширования зависит не только от индекса, который надо повторно хешировать, но также от первоначального ключа. Отметим, что значение h2(key) не нужно еще раз вычислять при каждом повторном хешировании: его необходимо вычислить только один раз для каждого ключа, который надо повторно хешировать. Следовательно, в оптимальном случае функции h1 и h2 должны быть выбраны так, чтобы они выполняли хеширование и повторное хеширование равномерно в интервале от 0 до N-1, а также минимизировали скучивание. Такие функции не всегда просто найти.

Кроме линейного опробывания существует несколько других схем с открытой адресацией. Рассмотрим две из них.

При использовании алгоритма квадратичного опробывания (quadratic probing) поиск точки вставки элемента осуществляется путем проверки не следующей по порядку ячейки, а ячеек, которые расположены все дальше от исходной. Если первое хеширование ключа оказывается безрезультатным и ячейка занята, то проверяется следующая ячейка (элемент массива). В случае неудачи проверяется ячейка, которая расположена через четыре ячейки. Если и эта проверка неудачна, то проверяется ячейка расположенная через девять индексов и т. д., причем последующие повторные опробывания выполняются для ячеек, расположенных через 16, 25, 36 и так далее ячеек. Этот алгоритм позволяет предотвратить образование кластеров, однако он может приводить и к ряду нежелательных проблем.

Во-первых, если для многих ключей хеширование генерирует один и тот же индекс, то все их последовательности повторных опробываний будут выполняться вдоль одного и того же пути. В результате образуется кластер, но такой, который кажется распределенным по хеш-таблице. Во-вторых, квадратичное опробывание не гарантирует посещения всех ячеек. Максимум в чем можно быть уверенным, если размер таблицы равен простому числу, это в том, что квадратичное опробывание обеспечит посещение, по меньшей мере, половины всех ячеек хеш-таблицы.

Следующая схема с открытой адресацией - псевдослучайное опробывание (pseudorandom probing). Этот алгоритм требует наличия программного датчика случайных чисел, начальное значение которого можно устанавливать в любой момент. Алгоритм устанавливает следующую последовательность действий. Выполняется первоначальное хеширование ключа, и полученное хеш-значение, передается в датчик псевдослучайных чисел в качестве его начального значения. Генерируется первое вещественное случайное число в диапазоне [0, 1], и оно умножается на размер таблицы (N) для получения целочисленного значения в диапазоне от 0 до N-1. Это значение и будет индексом проверяемого элемента. Если ячейка занята, то генерируется следующее случайное число, умножается на размер таблицы, и ячейка с полученным значением индекса проверяется. Этот процесс выполняется до тех пор, пока не будет найдена пустая ячейка. Поскольку для одного и того же начального значения генератор будет генерировать одни и те же числа в одной и той же последовательности, для одного и того же хеш-значения всегда будет создаваться одна и та же последовательность опробывания.

12.3.2 Разрешение коллизий методом цепочек

Имеется несколько причин, почему повторное хеширование может быть неадекватным методом для обработки коллизий при хешировании. Во-первых, оно предполагает фиксированный размер таблицы. Если число записей превысит этот размер, то невозможно выполнять вставки без выделения таблицы большего размера и повторного вычисления значений хеширования для ключей всех записей, находящихся уже в таблице, используя новую хеш-функцию. Более того, из такой таблицы трудно удалить запись. Например, предположим, что в позиции рosInd находится запись Rec1. При добавлении некоторой записи Rec2, чей ключ k2 хешируется в рosInd, эта запись должна быть вставлена в первую свободную позицию rh(рosInd), rh(rh(рosInd)), .... Предположим, что Rec1 затем удаляется, так что ячейка с индексом рosInd становится свободной. Поиск записи Rec2 начинается с позиции h(k2), что равно рosInd. Но поскольку эта позиция уже свободна, процесс поиска может ошибочно сделать вывод, что записи Rec2 нет в таблице.

Одно возможное решение этой проблемы состоит в маркировании удаленной записи как «удаленная» (логическое удаление), а не «свободная», и продолжении поиска, когда встречается такая «удаленная» позиция. Но это реально, если только выполняется небольшое число удалений. В противном случае при неудачном поиске придется организовать поиск по всей таблице, потому что большинство позиций будет отмечено как «удаленные», а не «свободные».

Другой метод разрешения коллизий при хешировании называетсяметодомцепочек или методом, использующим связывание (chaining). Он представляет собой организацию связанного списка (цепочки) из всех записей, чьи ключи хешируются в одно и то же значение. Предположим, что хеш-функция выдает значения в диапазоне от 0 до N-1. Тогда описывается некоторый массив arrHeader, имеющий размер N и состоящий из узлов заголовков. Элемент arrHeader[i] указывает на список всех записей, чьи ключи хешируются в i.

Вставка c помощью хеширования осуществляет доступ к заголовку списка arrHeader[k], где k = h(Key). Затем производится вставка элемента с ключом Key в k-ый список. На рисунке 12.2 показан метод цепочек. Предполагается, что имеется массив заголовков из 10 элементов и что хеш-функция равна Key Mod 10. Предполагается также, что включение очередного элемента производится в конец списка. На рисунке представлен пример поступления ключей в таком порядке:

75, 66, 42, 192, 91, 40, 49, 87, 67, 16, 417, 130, 372, 227

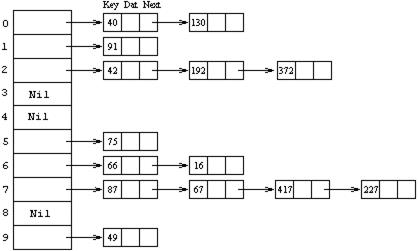
Рисунок 12.2 - Разрешение коллизий методом цепочек

Удаление узла из таблицы, которая построена по методу цепочек, заключается просто в исключении узла из связанного списка. Удаленный узел никак не влияет на эффективность алгоритма поиска. Алгоритм будет работать так, как если бы этот узел никогда не вставлялся в таблицу. Отметим, что эти списки могут быть динамически переупорядочены для получения большей эффективности поиска.

Поиск выполняется очень просто: сначала аргумент поиска ArgSearch хешируется в некоторый индекс, допустим в индекс k, а затем в k-ом списке осуществляется поиск ключа, равного значению ArgSearch.

Основным недостатком метода цепочек является то, что для узлов указателей требуется дополнительное пространство памяти. Однако в алгоритмах, которые используют метод цепочек, первоначальный массив меньше, чем в алгоритмах, которые используют повторное хеширование. Это происходит из-за того, что при методе цепочек ситуация не становится критичной, если весь массив становится заполненным. Всегда имеется возможность выделить дополнительные узлы и добавить их к различным спискам. Конечно, если эти списки станут очень длинными, то теряет смысл вся идея хеширования.