Красно-черные деревья

13.2.1 Определение красно-черного дерева, структура его элементов

Красно-черные деревья представляет собой одну из множества сбалансированных схем деревьев поиска, которые гарантируют время выполнения операций над динамическим множеством О(log(N)) даже в наихудшем случае.

В 1978 году Гюиба и Седжвик предложили концепцию красно-черного дерева. Красно-черные деревья (RB-деревья) – это структуры данных, используемые для реализации карт преобразования данных в библиотеке стандартных шаблонов Си++. Красно-черный алгоритм предоставляет быстрый и эффективный метод балансировки дерева бинарного поиска, требующий для каждой вершины не слишком много дополнительного объема памяти для хранения информации, необходимой для балансировки.

Красно-черное дерево представляет собой бинарное дерево поиска с одним дополнительным полем цвета каждой вершины. Цвет вершины может быть либо красным, либо черным. В соответствии с ограничениями, накладываемыми на вершины дерева, красно-черные деревья являются приближенно сбалансированными.

Каждая вершина дерева содержит поля color, left, right, parent и информационные поля, среди которых выделим поле ключа Key. Если у некоторой вершины не существует дочерней вершины или родителя, то соответствующие указатели left, right или parent принимают значения Nil. Эти значения Nil рассматриваются как указатели на внешние вершины (естественно несуществующие, фиктивные). Внешние вершины, следовательно, являются листьями. При этом все обычные вершины, содержащие поле ключа, определяются как внутренние вершины.

Бинарное дерево поиска является красно-черным деревом, если оно удовлетворяет следующим красно-черным свойствам:

1) каждая вершина является красной или черной;

2) корень дерева является черным;

3) каждая внешняя вершина является черной;

4) если вершина – красная, то обе ее дочерние вершины – черные;

5) для каждой вершины все пути от нее до листьев, являющихся потомками данной вершины, содержит одно и то же количество черных вершин.

На рисунке 13.6 показан пример красно-черного дерева.

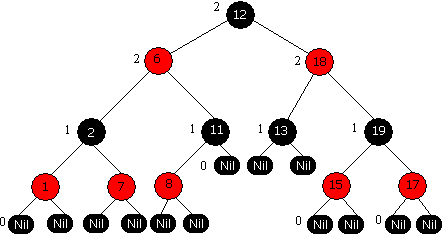
Рисунок 13.6 – Пример красно-черного дерева

Количество черных вершин на пути от вершины z (не считая саму вершину) к листу называется черной высотой вершины (black-height) и обозначается bh(z). На рисунке 13.6 возле некоторых вершин указана их черная высота.

В соответствии со свойством 5 красно-черных деревьев, черная высота вершины – точно определяемое значение. Черной высотой дерева считается черная высота ее корня.

Для красно-черного дерева справедливо следующее утверждение: красно-черное дерево с N внутренними вершинами имеет высоту не более чем 2lg(N + 1).

Непосредственным следствием данного утверждения является то, что базовые операции на динамическими множествами при использовании красно-черных деревьев выполняются за время О(log(N))., поскольку, как показано в подразделе 13.1, время выполнения этих операций высотой h составляет О(h), а любое красно-черное дерево с N вершинами является деревом поиска высотой 2lg(N + 1).

13.2.2 Повороты

Операции вставки и удаления, будучи применены к красно-черному дереву с N вершинами изменяют дерево. В результате выполнения этих операций могут нарушаться красно-черные свойства, перечисленные ранее. Для восстановления этих свойств необходимо изменить цвета некоторых вершин, а также структуру его указателей.

Изменения в структуре указателей выполняются при помощи поворотов (rotations), которые представляют собой локальные операции в дереве поиска, сохраняющие свойство бинарного дерева поиска. На рисунке 13.7 показаны два типа поворотов – левый и правый (здесь a, b и g – произвольные поддеревья). При выполнении левого поворота в вершине х предполагается, что ее правая дочерняя вершина y не является листом. Левый поворот выполняется «вокруг» связи между х и y, делая y новым корнем поддерева, левой дочерней вершиной которого становится х, а бывший левый сын вершины y – правым сыном х.

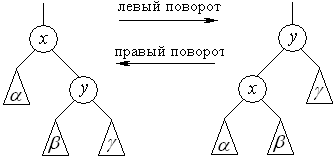
Рисунок 13.7 – Операции поворота в бинарном дереве

При повороте изменяются только указатели, все остальные поля сохраняют свое значение.

Литература

1. Бакнелл Д.М. Фундаментальные алгоритмы и структуры данных в Delphi. - СПб: ООО «ДиаСофтЮП», 2003. - 506 с.

2. Вирт Н. Алгоритмы и структуры данных. - СПб: Невский диалект, 2001. – 352 с.

3. Гудрич М. Т. Структуры данных и алгоритмы в Java. / М. Т. Гудрич, Р. Тамассия. – Мн.: Новое знание, 2003. – 671 с.

4. Кормен Т. Х., Лейзерсон Ч. И., Ривест Р. Л., Штайн К. Алгоритмы: построение и анализ. – М.: Издательский дом «Вильямс», 2009. – 1296 с.

5. Круз Р. Л. Структуры данных и проектирование программ. – М.: БИНОМ. Лаборатория знаний, 2008. – 765 с.

6. Седжвик Р. Фундаментальные алгоритмы на С. Части 1-4: Анализ / Структуры данных / Сортировка / Поиск. - К.: Издательство «ДиаСофт», 2003. - 672 с.

7. Седжвик Р. Фундаментальные алгоритмы на С. Часть 5: Алгоритмы на графах. - К.: Издательство «ДиаСофт», 2003. - 496 с.

8. Архангельский А.Я. Программирование в Delphi 6. - М.: ЗАО «Издательсво БИНОМ», 2002. - 1120 с.

9. Гетц К., Гилберт М. Программирование на Visual Basic 6 и VBA. Руководство разработчика. - К.: Издательская группа BHV, 2001. - 912 с.

10. Гук М. Аппаратные средства IBM PC. Энциклопедия. - СПб: Питер, 2003. - 928 с.

11. Кнут Д. Э. Искусство программирования, том 1. Основные алгоритмы. - М.: Издательский дом «Вильямс», 2002. - 720 с.

12. Кнут Д. Э. Искусство программирования, том 3. Сортировка и поиск. - М.: Издательский дом «Вильямс», 2001. - 832 с.

13. Либерти Д. Освой самостоятельно С++ за 21 день. - М.: Издательский дом «Вильямс», 2002. - 832 с.

14. Лэнгсам Й., Огенстайн М., Тененбаум А. Структура данных для персональных ЭВМ. – М.: Мир, 1989. – 475 с.

15. Системное программное обеспечение / А.В. Гордеев, А.Ю. Молчанов - СПб: Питер, 2003. - 736 с.

16. Структуры и организация данных в компьютере. Учебное пособие / Лакин В.И., Романов А.В. – Мн.: НПООО «Пион», 2001 – 160 с.