B-деревья

Видимо, наиболее популярным подходом к организации индексов в базах данных является использование техники B-деревьев. B-дерево содержит по одному индексному элементу для каждой строки таблицы, в которой имеется непустое (NOT NULL) индексное значение. С точки зрения внешнего логического представления B-дерево - это сбалансированное сильно ветвистое дерево во внешней памяти (рис.5.3).

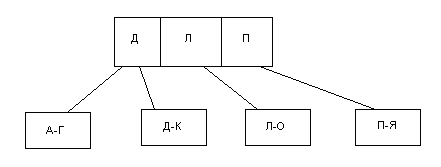Рис. 5.3 - Древовидный индекс по текстовому столбцу

С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, т.е. каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.

В типовом случае структура внутренней страницы выглядит следующим образом:

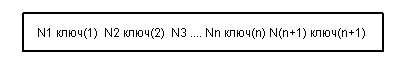
При этом выдерживаются следующие свойства:

ключ(1) <= ключ(2) <= ... <= ключ(n);

в странице дерева Nm находятся ключи k со значениями ключ(m) <= k <= ключ(m+1).

Листовая страница обычно содержит значение индекса и идентификаторы строк (ROWID) и имеет следующую структуру:

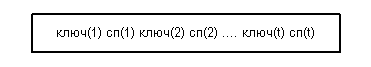
Листовая страница обладает следующими свойствами:

· ключ(1) < ключ(2) < ... < ключ(t);

· сп(r) - упорядоченный список идентификаторов кортежей (tid), включающих значение ключ(r);

· листовые страницы связаны одно- или двунаправленным списком.

Поиск в B-дереве - это прохождение от корня к листу в соответствии с заданным значением ключа. Заметим, что поскольку деревья сильно ветвистые и сбалансированные, то для выполнения поиска по любому значению ключа потребуется одно и то же (и обычно небольшое) число обменов с внешней памятью. Более точно, в сбалансированном дереве, где длины всех путей от корня к листу одни и те же, если во внутренней странице помещается n ключей, то при хранении m записей требуется дерево глубиной log_n(m). Если n достаточно велико (обычный случай), то глубина дерева невелика, и производится быстрый поиск.

Основной "изюминкой" B-деревьев является автоматическое поддержание свойства сбалансированности. Рассмотрим, как это делается при выполнении операций занесения и удаления записей.

При занесение новой записи выполняется:

· Поиск листовой страницы. Фактически, производится обычный поиск по ключу. Если в B-дереве не содержится ключ с заданным значением, то будет получен номер страницы, в которой ему надлежит содержаться, и соответствующие координаты внутри страницы.

· Помещение записи на место. Естественно, что вся работа производится в буферах оперативной памяти. Листовая страница, в которую требуется занести запись, считывается в буфер, и в нем выполняется операция вставки. Размер буфера должен превышать размер страницы внешней памяти.

· Если после выполнения вставки новой записи размер используемой части буфера не превосходит размера страницы, то на этом выполнение операции занесения записи заканчивается. Буфер может быть немедленно вытолкнут во внешнюю память, или временно сохранен в оперативной памяти в зависимости от политики управления буферами.

· Если же возникло переполнение буфера (т.е. размер его используемой части превосходит размер страницы), то выполняется расщепление страницы. Для этого запрашивается новая страница внешней памяти, используемая часть буфера разбивается, грубо говоря, пополам (так, чтобы вторая половина также начиналась с ключа), и вторая половина записывается во вновь выделенную страницу, а в старой странице модифицируется значение размера свободной памяти. Естественно, модифицируются ссылки по списку листовых страниц.

· Чтобы обеспечить доступ от корня дерева к заново заведенной странице, необходимо соответствующим образом модифицировать внутреннюю страницу, являющуюся предком ранее существовавшей листовой страницы, т.е. вставить в нее соответствующее значение ключа и ссылку на новую страницу. При выполнении этого действия может снова произойти переполнение теперь уже внутренней страницы, и она будет расщеплена на две. В результате потребуется вставить значение ключа и ссылку на новую страницу во внутреннюю страницу-предка выше по иерархии и т.д.

· Предельным случаем является переполнение корневой страницы B-дерева. В этом случае она тоже расщепляется на две, и заводится новая корневая страница дерева, т.е. его глубина увеличивается на единицу.

При удалении записи выполняются следующие действия:

· Поиск записи по ключу. Если запись не найдена, то удалять ничего не нужно.

· Реальное удаление записи в буфере, в который прочитана соответствующая листовая страница.

· Если после выполнения этой подоперации размер занятой в буфере области оказывается таковым, что его сумма с размером занятой области в листовых страницах, являющихся левым или правым братом данной страницы, больше, чем размер страницы, операция завершается.

· Иначе производится слияние с правым или левым братом, т.е. в буфере производится новый образ страницы, содержащей общую информацию из данной страницы и ее левого или правого брата. Ставшая ненужной листовая страница заносится в список свободных страниц. Соответствующим образом корректируется список листовых страниц.

· Чтобы устранить возможность доступа от корня к освобожденной странице, нужно удалить соответствующее значение ключа и ссылку на освобожденную страницу из внутренней страницы - ее предка. При этом может возникнуть потребность в слиянии этой страницы с ее левым или правыми братьями и т.д.

· Предельным случаем является полное опустошение корневой страницы дерева, которое возможно после слияния последних двух потомков корня. В этом случае корневая страница освобождается, а глубина дерева уменьшается на единицу.

Как видно, при выполнении операций вставки и удаления свойство сбалансированности B-дерева сохраняется, а внешняя память расходуется достаточно экономно.

Проблемой является то, что при выполнении операций модификации слишком часто могут возникать расщепления и слияния. Чтобы добиться эффективного использования внешней памяти с минимизацией числа расщеплений и слияний, применяются более сложные приемы, в том числе:

· упреждающие расщепления, т.е. расщепления страницы не при ее переполнении, а несколько раньше, когда степень заполненности страницы достигает некоторого уровня;

· переливания, т.е. поддержание равновесного заполнения соседних страниц;

· слияния 3-в-2, т.е. порождение двух листовых страниц на основе содержимого трех соседних.

Следует заметить, что при организации мультидоступа к B-деревьям, характерного при их использовании в СУБД, приходится решать ряд нетривиальных проблем. Конечно, грубые решения очевидны, например монопольный захват B-дерева на все выполнение операции модификации. Но существуют и более тонкие решения.

Сбалансированное дерево автоматически не уравновешивает распределение ключей в пределах дерева так, чтобы половина ключей находилась бы на одной стороне В-дерева, а другая половина — на другой. Очевидно, что нет необходимости перестраивать дерево всякий раз, когда добавляются или удаляются ключи. Однако если ключи добавляются или удаляются только на одной стороне дерева, то распределение индексных ключей может стать неравномерным, с изрядным числом разреженных и даже опустошенных блоков по одну сторону дерева. В этом случае индекс рекомендуется перестроить.

На В-деревьях для извлечения данных по запросу может использоваться механизм быстрого полного просмотра (fast full scan). Этот механизм дает существенные преимущества, если все запрошенные из конкретной таблицы данные могут быть получены только из индекса. При быстром полном просмотре эффективный многоблочный ввод/вывод, обычно применяемый для полных просмотров таблиц, используется для прочтения всех листовых блоков В-дерева. Поскольку число листовых блоков индекса, скорее всего, намного меньше, чем блоков данных в таблице, для выполнения запроса требуется просмотреть меньшее число блоков. Поэтому просмотр индекса совершится значительно быстрее, чем полный просмотр таблицы, хотя иногда неравномерное распределение ключей снижает эффективность быстрого полного просмотра, поскольку требуется просмотреть большее число листовых блоков (содержащих малое или вообще нулевое число элементов). При этом следует учитывать наличие или отсутствие в таблице пустых значений, которые, как было сказано выше, в индекс не заносятся.

В-деревья можно использовать для поиска данных, как по условиям равенства, так и по условиям неравенства. Это единственный тип индексов, который можно использовать для предикатов неравенства: LIKE, BETWEEN, “>”, “>=”, “<”, “<=”. Исключение представляет случай использования предиката LIKE при сравнении с шаблоном вида ‘%выражение’ или ‘_выражение’. В-деревья хранят только непустые значения ключей, так что можно построить разреженное В-дерево.