Бинарные деревья поиска

Бинарным деревом поиска называется бинарное дерево из элементов, в котором ключ элемента в каждой вершине больше ключей всех элементов левого поддерева и меньше ключей элементов правого поддерева. Ниже приведен пример бинарного дерева поиска с числовыми значениями ключей.

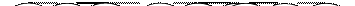
Можно схему бинарного поиска в таблице, упорядоченной по возрастанию ключей, представить деревом поиска. В корне будет находиться элемент со средним индексом, элементы со средними индексами верхней и нижней половин таблицы составят значения левого и правого сыновей корня, следующий уровень вершин составят средние элементы всех четвертей таблицы и так далее.

Дерево поиска удобно для нахождения элемента с заданным ключом. Этот ключ сначала сравнивается с ключом корня. Если ключ корня больше, то переходим к левому сыну корня, иначе – к правому. Процесс продолжается в направлении от корня к листьям до нахождения элемента или получения отрицательного результата.

Деревья поиска применяют, например, в трансляторах для хранения и быстрого поиска ключевых слов или идентификаторов программы.

Наряду с поиском деревья поиска обеспечивают сортировку элементов. Действительно, обход дерева в порядке слева направо дает перечисление элементов по возрастанию ключей.

Включение нового элемента в дерево поиска выполняется следующим образом. Сначала производится поиск элемента с ключом, равным ключу нового элемента. После прихода в лист элемент войдет в новую вершину дерева, которая будет левым или правым сыном найденного листа в зависимости от значения ключа элемента.

Удаление элемента из дерева поиска предполагает такую перестройку дерева, чтобы оно не содержало указанного элемента, но оставалось деревом поиска. Возможны следующие три случая при удалении элемента из дерева поиска.

1. Удаляемый элемент находится в листе дерева. В этом случае удаляется соответствующая ссылка из отцовской вершины.

2. Удаляемый элемент находится в вершине с одним сыном. На место вершины с данным элементом помещается ее единственный сын со всеми своими потомками, то есть подтягивается все поддерево по имеющейся ветви.

3. Удаляемый элемент находится в вершине с обоими сыновьями. Сначала на место удаляемого элемента помещается один из двух элементов с соседними значениями ключа. Это может быть элемент с меньшим значением ключа из самой правой вершины левого поддерева либо с большим значением ключа из самой левой вершины правого поддерева. Для нахождения вершины с этим элементом достаточно спуститься из вершины с удаляемым элементом по левой ветви и далее идти по правым ветвям, пока это возможно, либо аналогичным образом найти этот элемент в правом поддереве. Найденная вершина имеет не более одного сына, поэтому дальнейшие действия сводятся к одному из первых двух случаев.

Например, удаление элемента с ключом 20 из дерева поиска, приведенного выше, даст следующий результат

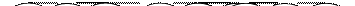
Рассмотрим следующую задачу. С клавиатуры вводится последовательность слов. Требуется последовательно включать эти слова в дерево поиска, учитывая число вхождений каждого слова. Далее обеспечить удаление некоторых слов. При удалении уменьшать счетчик числа повторений слова и полностью удалять слово при обнулении этого счетчика. После каждой операции выдавать дерево поиска на экран, перечисляя вершины по алфавиту слов с указанием уровня вершин и счетчика повторений.

Program PoiskVkl;

{ поиск с включением на бинарном дереве }

Uses Crt;

Type

ref= ^word;

word=record

Key: string;

Count: integer;

Left, Right: ref

end;

Var

Root: ref;

Rab: string;

B: boolean;

Procedure Search(X: string; var P: ref);

Begin

if P=Nil then { слова нет - включить ! }

begin

New(P);

with P^ do

begin

Key:=X;

Count:=1; Left:=Nil; Right:=Nil

end

end

else

if X<P^.Key then Search(X, P^.Left)

else

if X>P^.Key then Search(X, P^.Right)

else { нашли слово }

P^.Count:=P^.Count+1

End;

Procedure Delete(X: string; var P: ref);

{ память освобождается, описатель var - обязателен }

Var

Q: ref;

Procedure Del(var R: ref); { сначала R=Q^.Left }

{ замещение Q^ самым правым элементом левого поддерева }

Begin

if R^.Right<>Nil then Del(R^.Right)

else

begin { R-самая правая вершина левого поддерева }

Q^.key:=R^.Key;

Q^.Count:=R^.Count;

Q:=R;

R:=R^.Left; { подтянули левое поддерево }

Dispose(Q)

end

End;

Begin

if P=Nil then

WriteLn('Слова нет в дереве !')

else

if X<P^.Key then Delete(X, P^.Left)

else

if X>P^.Key then Delete(X, P^.Right)

else { X=P^.Key - нашли слово }

if P^.Count>1 then P^.Count:=P^.Count-1

else

begin { полное удаление слова }

Q:=P; { Q – указатель на удаляемую вершину }

if Q^.Right=Nil then

begin

P:=Q^.Left; { подтянули левое поддерево }

Dispose(Q)

{ работает, благодаря рекурсии: меняя P, меняется }

{ P^.Left или P^.Right у отцовской вершины }

end

else if Q^.Left=Nil then

begin

P:=Q^.Right; { подтянули правое поддерево }

Dispose(Q)

end

else Del(Q^.Left); { замена }

end

End;

Procedure PrintTree(W: ref; L: integer);

{ W-корень, L-число точек, показывающее уровень дерева }

Var

I: integer;

Begin

if W<>Nil then

with W^ do

begin

PrintTree(Left, L+1);

For I:=1 to L do

Write('.');

WriteLn(Key, ' ', Count);

PrintTree(Right, L+1)

end

End;

Begin

ClrScr;

Rab:=' ';

Root:=Nil;

B:=True;

While B do

begin

Write('Укажите слово для ввода (к-признак конца) ');

Readln(Rab);

if Rab<>'к' then

begin

Search(Rab, Root);

PrintTree(Root, 0)

end

else B:=False

end;

B:=True;

While B do

begin

Write('Укажите слово для удаления (к-признак конца) ');

Readln(Rab);

if Rab<>'к' then

begin

Delete(Rab, Root);

PrintTree(Root, 0)

end

else B:=False

end;

End.