Алгоритмы поиска кратчайших путей Дейкстры и Флойда
Обычно в практических задачах длина пути измеряется не числом дуг, а их суммарной длиной. Термин длина носит обобщенный смысл. Синонимами этого термина являются расстояние, вес, стоимость дуг, причем могут рассматриваться и отрицательные значения.
Рассмотрим два алгоритма поиска кратчайших путей между вершинами: Дейкстры и Флойда. Будем считать, что длина дуги из вершины Vi в вершину Vj задана элементом матрицы aij, причем aii=0 и aij =¥, если дуга из вершины Vi в вершину Vj отсутствует.
В алгоритме Дейкстры находится кратчайший путь из вершины S в вершину T. Вершинам присваиваются временные и окончательные метки, которые будем обозначать соответственно буквами C и D с индексами вершин.
1. Вершине S присваивается окончательная метка 0, то есть Cs:=0, временным меткам остальных вершин – значение ¥.
2. Пусть i – номер последней вершины, которой присвоена окончательная метка Ci. Каждой вершине j, имеющей временную метку Dj, присваивается новая временная метка по правилу Dj:=min(Ci+aij , Dj). Если значение Dj меняется, то вместе с ним сохраняется номер предыдущей вершины i.
3. Наименьшая из временных меток объявляется окончательной. Пусть k – номер этой вершины. Следовательно, Ck:=Dk. Если вершина T не получила окончательной метки, то i:=k и переход к 2.
4. Конец.
Полученная для вершины T окончательная метка дает величину кратчайшего пути. Сам путь восстанавливается от конца к началу и состоит из вершин, обеспечивших окончательные метки.
Пусть имеется следующий граф.
 3
3
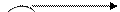 | |||
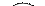 | |||
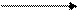
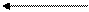 2
2
Требуется найти кратчайший путь из вершины A в вершину C.
Этапы расстановки меток удобно представить в виде таблицы. Окончательную метку будем отмечать жирным шрифтом и подчеркиванием. В скобках указывается предыдущая вершина.
| № шага | A | B | C | D |
| 0 | ¥ | ¥ | ¥ | |
| 0 | 1(A) | ¥ | 2(A) | |
| 0 | 1(A) | ¥ | 2(A) | |
| 0 | 1(A) | 4(B) | 2(A) | |
| 0 | 1(A) | 4(B) | 2A) | |
| 0 | 1(A) | 3(D) | 2(A) | |
| 0 | 1(A) | 3(D) | 2(A) |
Итак, длина кратчайшего пути равна 3. Окончательная метка 3 для вершины C получена из предыдущей вершины D. В свою очередь окончательная метка 2 для вершины D получена из вершины A. Следовательно, кратчайший путь составляют вершины A, D, C.
Значения окончательных меток появляются по возрастанию, то есть алгоритм Дейкстры обеспечивает поиск в ширину. Алгоритм не работоспособен при наличии отрицательных расстояний, что иллюстрирует следующий простой пример

 -3
-3
 1
1
Здесь кратчайший путь из A в C проходит через вершину B и равен -1, тогда как по алгоритму Дейкстры вершина C сразу получит окончательную метку 1.
Трудоемкость алгоритма Дейкстры пропорциональна величине N 2, где N – количество вершин графа.
Алгоритм Флойда определяет кратчайшие пути между всеми парами вершин. Снова будем считать, что длина дуги из вершины Vi в вершину Vj задана элементом матрицы aij, причем aii=0 и aij =¥, если дуга из вершины Vi в вершину Vj отсутствует.
Пусть элемент aij(k) матрицы A(k) равен длине кратчайшего пути из вершины Vi в вершину Vj, с номерами промежуточных вершин, не превосходящими k. Тогда выполняется рекуррентное соотношение
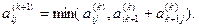 (*)
(*)
Действительно, кратчайший путь из Vi в Vj с номерами промежуточных вершин, не превосходящими k+1, может не проходить через вершину Vk+1 . В противном случае он представляет собой кратчайший путь из Vi в Vk+1, а затем из Vk+1 в Vj.
В качестве A(0) выбирается исходная матрица A. Матрица A(n) даст длины кратчайших путей между всеми парами вершин без каких-либо ограничений на промежуточные вершины. Значение aij(n) = ¥ означает отсутствие пути из вершины Vi в вершину Vj.
Параллельно с описанными матрицами строится последовательность матриц B(i) для нахождения самих кратчайших путей. Элемент bij(k) матрицы B(k) устанавливается равным номеру второй вершины на кратчайшем пути из Vi в Vj с номерами промежуточных вершин, не превосходящими k, и 0 в случае отсутствия путей. Элемент bij(k+1) не меняется, если в формуле (*) минимум достигается на первом значении, и полагается равным bik+1(k), если минимально второе выражение, так как в этом случае кратчайший путь проходит через вершину Vk+1.
Первоначально bij(0) матрицы B(0) полагается равным j, если есть дуга из Vi в Vj, и 0, если такая дуга отсутствует. Матрица B(n) позволяет восстановить кратчайший путь между любыми двумя вершинами. Действительно, если s=bij(n) дает вторую вершину на кратчайшем пути из Vi в Vj, то t=bsj(n) даст третью вершину, w=btj(n) - четвертую и так далее до попадания в вершину Vj. Значение bij(n) =0 означает отсутствие пути из вершины Vi в вершину Vj.
Рассмотрим в качестве примера следующий граф, в котором вершины идентифицированы номерами
 3
3
 1
1
Для него матрицы A(0) и B(0) имеют соответственно вид
| ¥ | |||
| ¥ | ¥ | ||
| ¥ | ¥ | ||
| ¥ |
На первом шаге допускаются пути, проходящие через вершину 1. Поскольку появляется путь 4-2-1, изменения затронут вторые элементы четвертой строки, то есть матрицы A(1) и B(1) примут вид
| ¥ | |||
| ¥ | ¥ | ||
| ¥ | ¥ | ||
На втором шаге допускаются пути, проходящие через вершины 1 и 2. Добавляются пути 1-2-3 и 4-1-2-3. Последний путь имеет большую длину, чем имеющаяся дуга 4-3, поэтому матрицы A(2) и B(2) примут вид
| ¥ | ¥ | ||
| ¥ | ¥ | ||
и так далее. Кратчайшие пути между всеми парами вершин будут представлены следующими матрицами A(4) и B(4)
Дата добавления: 2015-08-21; просмотров: 1871;
