Поиск путей

Обходом графа называют посещение всех его вершин и ребер. Проще всего осуществляется обход в глубину с помощью стека.

Пусть граф неориентирован. Чтобы не путать вершину стека с вершинами графа, будем называть последние узлами. Пройденные узлы графа помечаются. В стеке хранится текущий путь, который инициализируется произвольным начальным узлом. Если из узла, находящегося в вершине стека, имеется ребро в непройденный узел, то этот узел помечается как пройденный и включается в стек. Исключение из стека происходит после прохождения всех ребер узла. Если стек становится пустым, процесс продолжается с какого-либо непомеченного узла. Трудоемкость обхода в глубину пропорциональна количеству ребер графа.

Вероятно, самой распространенной задачей на графах является поиск путей без циклов между заданными вершинами. Он может быть реализован на основе обхода в глубину. Если требуются все пути, вершины могут посещаться неоднократно. В этом случае пройденные вершины рассматриваются только для текущего пути. Исключение из стека происходит также после нахождения очередного пути. Описанный подход распространяется и для ориентированных графов. Такой способ нахождения решения является примером применения алгоритма с возвратами.

Трудоемкость перечисления всех путей на основе приведенного метода может быть очень высокой. Так для графа из N вершин, в котором каждая пара вершин связана ребром, число путей между двумя заданными вершинами оценивается астрономической величиной (N-2)! + (N-3)! + ….+ 2! + 1.

Приведем текст соответствующей программы.

Program Puti; { поиск путей в глубину на ориентированном графе }

Uses crt;

Const

max=10;

Type

mat=array[1..max,1..max] of integer; { матрица смежности }

put=1..max; { номер вершины в пути }

Var

matr : mat;

gr: array [1..max] of integer; { текущий путь }

zapret: array [1..max] of boolean;

{ запрет вершин: false-вершина запрещена }

a,b,ver,k,j,i: integer;

l: boolean;

ch: char;

Procedure ReadMat(var matr: mat);

{ ввод матрицы смежности }

Begin

TextBackGround(Black);

TextColor(White);

Clrscr;

Write('Введите количество вершин: ');

Readln(ver);

For i:=1 to ver do

For j:=1 to ver do

begin

matr[i,j]:=0;

matr[j,i]:=0

end;

Repeat

Write('Введите связи в виде пары вершин (99-конец) ');

Read(i);

if i<>99 then Read(j);

if (i>0) and (i<=ver) and (j>0) and (j<=ver) then

matr[i,j]:=1

else if i<>99 then Writeln('Ошибка ввода ')

Until i=99;

Writeln('Ввод закончен !');

Writeln;

Readln { пауза }

End;

Procedure Wiwod(matr: mat);

Begin

Window(46,2,75,22); { окно вывода результатов }

TextBackGround(Cyan);

Clrscr;

TextColor(LightGreen);

Write(' ');

For i:=1 to ver do

Write(i:2); { номера столбцов матрицы }

Writeln;

For i:=1 to ver do

begin

TextColor(LightGreen);

Write(i:2); { номера строк матрицы }

TextColor(White);

For j:=1 to ver do

Write(matr[i,j]:2);

Writeln

end

End;

Procedure PoiskPut(t: integer);

{ поиск всех путей на графе }

Var i: integer;

Begin

gr[j]:=t; { добавление в путь текущей вершины }

Zapret[t]:=false;

j:=j+1;

if t=b then { b-конечная вершина }

begin

Write('Найден путь: ');

For i:=1 to j-1 do { вывод пути }

Write(gr[i],' ');

Writeln;

Readln; { пауза }

end

else

For i:=1 to ver do

if Zapret[i] and (matr[t,i]=1) then

{ поиск в глубину: выбор продолжения пути без цикла }

PoiskPut(i);

{ здесь оказываемся после нахождения очередного пути }

{ или в случае попадания в тупик }

{ исключение из множества вершин пути последней вершины }

j:=j-1; { возврат в предыдущую вершину }

Zapret[t]:=true; {снятие зппрета}

End;

Begin { основная программа }

Clrscr; { очистка экрана }

ReadMat(matr); { ввод матрицы смежности }

l:=true;

While l do

begin

Wiwod(matr);

Writeln;

Write('Введите начальную вершину: ');

Readln(a);

Write('Введите конечную вершину: ');

Readln(b);

Writeln;

For i:=1 to ver do

Zapret[i]:=true; {все вершшины сначала разрешены}

j:=1;

PoiskPut(a); { перечисление всех путей }

Writeln('Путей больше нет ! ');

Write('Повторить поиск[д/н] ? ');

Readln(ch);

if ch='н' then l:=false { для выхода из цикла }

end

End.

В этой прграмме стек реализуется с помощью рекурсии. Рассмотрим порядок нахождения путей на примере. Пусть имеется граф

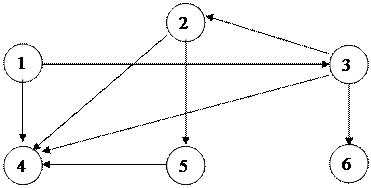и требуется перечислить пути из вершины 1 в вершину 4. В процессе поиска в стеке будут находиться следующие номера вершин:

· 1;

· 1,3;

· 1,3,2;

· 1,3,2,4;

· 1,3,2;

· 1,3,2,5;

· 1,3,2,5,4;

· 1,3,2,5;

· 1,3,2;

· 1,3,4;

· 1,3;

· 1,3,6;

· 1,3;

· 1;

· 1,4;

· 1;

· Æ.

Последовательность обхода вершин графа можно представить деревом

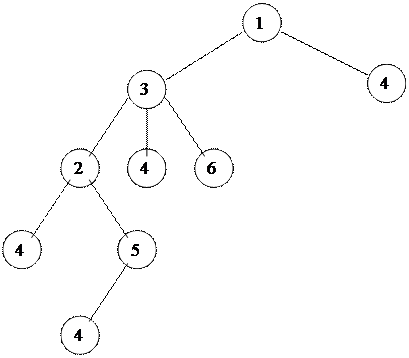Корнем дерева является начальная вершина, а листьями – конечная вершина либо тупиковые вершины, из которых нет продолжения пути без циклов. Последовательность нахождения путей соответствует обходу дерева в порядке сверху вниз.