Балансировка деревьев поиска

Трудоемкость нахождения заданного элемента в дереве поиска зависит от структуры этого дерева. Например, если ни у одной вершины нет левого сына, то дерево вырождается в линейный список, и поиск сводится к последовательному перебору вершин. В связи с этим появляется необходимость в поддержке определенной сбалансированности дерева поиска.

По определению Вирта, дерево поиска является идеально сбалансированным, если для каждой его вершины количество вершин в левом и правом поддеревьях отличается не более, чем на 1.

В процессе корректировки идеальная балансировка дерева часто нарушается. Имеется более мягкое определение: дерево сбалансированно, если высота (глубина, количество уровней) левого и правого поддеревьев любой вершины отличается не более, чем на 1. Сбалансированные деревья поиска называют АВЛ-деревьями по именам авторов Адельсон-Вельского и Ландиса. В АВЛ-деревьях необходимость в операциях балансировки появляется реже, а сами эти операции достаточно просты.

Восстановление баланса в АВЛ-деревьях достигается путем преобразований, называемых поворотами. Имеются четыре типа поворотов: LL-поворот, RR-поворот, LR-поворот и RL-поворот. Первые два из них считаются одинарными, а последние два – двойными. Это связано с количеством операций, необходимых для восстановления баланса.

Мнемонические обозначения типов поворота связаны с ситуациями нарушения баланса, возникающими в некоторой вершине в результате включения новой вершины. Если оказывается, что в этой вершине высота левого поддерева больше на 2 уровня высоты правого поддерева, то первой буквой в мнемоническом обозначении поворота будет L. Если для левого сына этой вершины высота левого поддерева остается большей, то потребуется LL-поворот. Аналогично определяются обозначения других типов поворотов.

Рассмотрим следующие примеры. Пусть имеется АВЛ-дерево

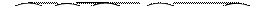
и включается элемент с ключом 4 или 7. В результате LL-поворота получится дерево

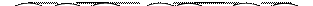
или

Если же в исходное дерево включается элемент с ключом 12 или 17, то LR-поворот приведет к дереву

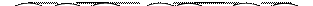
или

Пусть дерево описано в виде динамической структуры с указателями Left и Right на левого и правого сыновей для каждой вершины, а указатель P показывает на вершину, в которой возникло нарушение баланса. Тогда LL-поворот выражается тремя операторами

P1:=P^.Left;

P^.Left:=P1^.Right;

P1^.Right:=P;

а LR-поворот шестью операторами

P1:=P^.Left; P2:=P1^.Right;

P1^.Right:= P2^.Left; P2^.Left:=P1;

P^.Left:=P2^.Right; P2^.Right:=P;

Рассмотрим примеры более сложных деревьев. Пусть имеется дерево

При включении элемента с ключом 1 или 3 потребуется LL-поворот в вершине с ключом 20, который в соответствии с указанными операторами приведет к дереву

или

При включении же элемента с ключом 11 или 14 потребуется LR-поворот, приводящий к дереву

или

Исключение из АВЛ-дерева несколько сложнее. Сначала исключение выполняется, как из обычного дерева поиска. Затем анализируется, есть ли нарушения баланса по направлению к корню дерева. Отличие от включения состоит в том, что балансировка может потребоваться более одного раза.

Рассмотрим в качестве примера следующее дерево.

Это дерево Фибоначчи: АВЛ-дерево заданной высоты с минимальным числом вершин. При удалении вершины с ключом 35 возникает нарушение баланса в вершине с ключом 30. LL-поворот приводит к новому нарушению баланса в корне дерева. В результате еще одного LL-поворота получается дерево

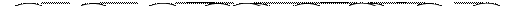
При удалении из АВЛ-дерева встречаются ситуации, когда восстановление баланса можно достигнуть как одинарным, так и двойным поворотом. Например, при удалении элемента с ключом 25 из дерева

баланс в корне дерева можно восстановить как LL-поворотом, так и LR-поворотом.