Then Begin
x:= a[j+1];
a[j+1]:= a[j];
a[j]:= x;
End
Else break;
End;
End;
11.2.2 Сортировка бинарными включениями
Алгоритм сортировки простыми включениями можно легко улучшить, пользуясь тем, что готовая последовательность a[0], ..., a[i-1], в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти быстрее, применив бинарный поиск, который определяет срединный элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения. Модифицированный алгоритм сортировки называется сортировкой бинарными включениями, он показан в следующей программе:
Рrocedure BinInsSort;
Var i, j, L, R, m: Integer;
x: TElement;
Begin
For i:=2 To N Do Begin
x:= a[i-1]; L:= 1; R:= i-1;
While L <= R Do Begin
m:= (L + R) Div 2;
If x.Кey < a[m-1].Кey Then R:= m - 1
Else L:= m + 1;
End;
For j:= i-1 Downto LDo a[j]:= a[j-1];
a[l-1]:= x;
End
End;
Сортировка включениями оказывается не очень подходящим методом для компьютеров: включение элемента с последующим сдвигом всего ряда элементов на одну позицию не экономна. Лучших результатов можно ожидать от метода, при котором пересылки элементов выполняются только для отдельных элементов и на большие расстояния. Эта мысль приводит к сортировке выбором.
11.2.3 Сортировка прямым выбором
Этот метод основан на следующем алгоритме:
- выбираем (выделяем) элемент с наименьшим (среди всех N элементов) ключом, допустим это элемент a[k]:
a[k].Key = min(a[0].Key, a[1].Key, …, a[HighIndex].Key)
- элемент a[k] меняется местами с первым элементом, т. е. с элементом a[0].
Затем выбираем элемент с наименьшим ключом среди всех элементов, кроме элемента a[0]; меняем его местами с элементом a[1] и т. д.
Эти операции затем повторяются с оставшимися N-2 элементами, затем с N-3 элементами, пока не останется только один элемент - наибольший. Метод, основанный на принципе пошагового выбора, продемонстрирован на тех же восьми ключах:

Обобщенно алгоритм прямого выбора можно представить следующим образом:
For i:=0 To HighIndexDo
Begin
<присвоить k индекс
наименьшего элемента из a[i], … a[HighIndex]>;
<поменять местами a[i] и a[k]>;
end;
Этот метод, называемый сортировкой прямым (простым) выбором, в некотором смысле противоположен сортировке простыми включениями; при сортировке простыми включениями на каждом шаге рассматривается только один очередной элемент входной последовательности и все элементы готового массива для нахождения места для включения; при сортировке простым выбором рассматриваются все элементы входного массива для нахождения элемента с наименьшим ключом, и этот один очередной элемент отправляется в готовую последовательность.
Обычно алгоритм сортировки простым выбором предпочтительней алгоритма сортировки простыми включениями, хотя в случае, когда ключи заранее упорядочены или почти упорядочены, сортировка простыми включениями все же работает несколько быстрее.
Весь алгоритм сортировки простым выбором реализован в следующей программе DirSelSort:
Рrocedure DirSelSort;
Var i, j, k: Integer;
x: TElement;
Begin
For i:=0 To HighIndex-1 Do Begin
x:=a[i]; k:= i;
For j:=i+1 To HighIndexDo
If x.Key > a[j].Key Then Begin
k:=j; x:=a[j];
End;
a[k]:=a[i]; a[i]:=x;
End
End;
11.2.4 Сортировка прямым обменом
Классификация методов сортировки не всегда четко определена. Методы прямого включения и прямого выбора используют в процессе сортировки обмен ключей. Однако теперь мы рассмотрим метод, в котором обмен двух элементов является основной характеристикой процесса. Приведенный ниже алгоритм сортировки простым обменом основан на принципе сравнения и обмена пары соседних элементов до тех пор, пока не будут рассортированы все элементы.
Если мы будем рассматривать массив, расположенный вертикально, а не горизонтально, и представим себе элементы пузырьками в резервуаре с водой, обладающими «весами», соответствующими их ключам, то каждый проход по массиву приводит к «всплыванию» пузырька на соответствующий его весу уровень. Этот метод широко известен как сортировка методомпузырька или пузырьковой сортировкой.
Проход метода начинается с конца сортируемого массива. Ключ последнего элемента a[HighIndex] сравнивается с ключом предпоследнего элемента a[HighIndex-1]. Если
a[HighIndex].Key < a[HighIndex-1].Key,
то сравниваемые элементы меняются местами друг с другом. Затем предпоследний элемент сравнивается с предыдущим, и если нужно, то происходит обмен и т. д. Следующий проход выполняется аналогичным образом. Сортировка завершается тогда, когда во время очередного прохода не произошло ни одного обмена.
Алгоритм пузырьковой сортировки иллюстрируется результатами выполнения проходов на тех же, что и ранее, ключах:
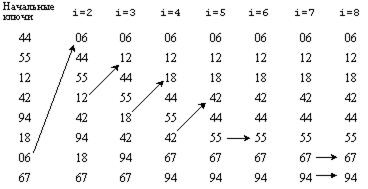
Простейшей реализацией пузырьковой сортировки является подпрограмма BubbleSort, показанная ниже:
Рrocedure BubbleSort;
Var i, j: Integer;
x: TElement;
flag: boolean;
Вegin
For i:= 1 To HighIndex Do Begin
// Начало прохода
flag:= True;
For j:= HighIndex DownTo i Do
If a[j-1].Key > a[j].Key Then Begin
flag:= False;
x:=a[j-1];
a[j-1]:=a[j];
a[j]:=x
end;
// Если обменов не было, то закончить
If flag Then Break;
End;
End;
В подпрограмме BubbleSort используется булева переменная flag, которая устанавливается в True в начале каждого прохода. Если при выполнении очередного прохода не было выполнено ни одного обмена, это означает, что массив a упорядочен. В этом случае переменная flag не изменяет своего значения и происходит выход из подпрограммы BubbleSort.
Внимательный читатель заметит здесь странную асимметрию: самый «легкий пузырек», расположенный в «тяжелом» конце неупорядоченного массива всплывет на нужное место за один проход, а «тяжелый пузырек», неправильно расположенный в «легком» конце будет опускаться на правильное место только на один шаг на каждом проходе. Например, массив
12, 18, 42, 44, 55, 67, 94, 06
будет рассортирован при помощи метода пузырька за один проход, а сортировка массива
94, 06, 12, 18, 42, 44, 55, 67
требует семи проходов, пока ключ 94 не окажется в конце массива. Эта неестественная асимметрия подсказывает следующее улучшение: менять направление следующих один за другим проходов. Полученный в результате алгоритм называют шейкер-сортировкой. Его работа показана на следующем примере:
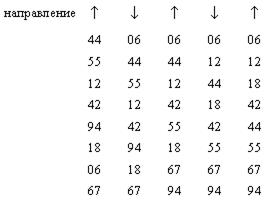
Из рисунка видно, что в результате первого прохода наверх переместился самый «легкий» ключ 06. А самый «тяжелый элемент», имеющий ключ 94, переместился на свое место уже на втором проходе, чего не наблюдалось при рассмотрении пузырьковой сортировки.
Анализ показывает, что сортировка обменом и ее небольшие улучшения хуже, чем сортировка включениями и выбором. Сортировка методом пузырька вряд ли имеет какие-то преимущества, кроме своего легко запоминающегося названия. Алгоритм шейкер-сортировки выгодно использовать в тех случаях, когда известно, что элементы уже почти упорядочены - редкий случай на практике.
Можно показать, что среднее расстояние, на которое должен переместиться каждый из N элементов во время сортировки, - это N/3 мест. Это число дает ключ к поиску усовершенствованных, т. е. более эффективных, методов сортировки. Все простые методы в принципе перемещают каждый элемент на одну позицию на каждом элементарном шаге. Поэтому они требуют порядка N2 таких шагов. Любое улучшение должно основываться на принципе пересылки элементов за один шаг на большое расстояние.
Текст подпрограммы шейкерной сортировки приводится ниже.
Procedure ShakerSort;
Var j, k ,L ,R: Integer;
x: TElement;
flag: boolean;
Begin
L:=1; R:= HighIndex; k:= R;
Repeat
flag:= true;
For j:=R DownTo L Do Begin
If a[j-1].Key > a[j].Key Then Begin
x:=a[j-1]; a[j-1]:=a[j]; a[j]:=x;
k:=j; flag:= false;
end;
End;
If flag Then Break;
L:=k+1;
flag:= True;
For j:=L To R Do
If a[j-1].Key > a[j].Key Then Begin
x:=a[j-1]; a[j-1]:=a[j]; a[j]:=x;
k:=j; flag:= false;
end;
If flag Then Break;
R:=k-1;
Until L > R
End;
11.2.5 Сортировка методом Шелла
Некоторое усовершенствование сортировки простыми включениями было предложено Д. Л. Шеллом в 1959 году. Этот метод показан на следующем примере.
Сортировка с убывающими расстояниями:
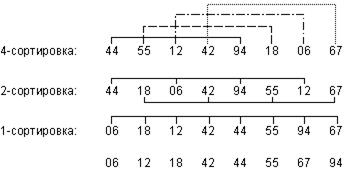
Расстоянием h между двумя элементами a[j] и a[i] называется положительная разность их индексов. Например, расстояние между элементами a[2] и a[6] равно 4 (h = 6-2).
На первом проходе отдельно группируются и сортируются (внутри группы) методом простого включения все элементы, отстоящие друг от друга на четыре позиции. Этот процесс называется 4-сортировкой. В нашем примере из восьми элементов каждая группа на первом проходе содержит ровно два элемента. После этого элементы вновь объединяются в группы с элементами, расстояние между которыми равно 2, и сортируются заново. Этот процесс называется 2-сортировкой. Наконец на третьем проходе все элементы сортируются обычной сортировкой включением (1-сортировка). Заметим, что группы, в которых последовательные элементы отстоят на одинаковые расстояния, никуда не передаются - они остаются «на том же месте».
На каждом шаге в сортировке участвует либо сравнительно мало элементов, либо они уже довольно хорошо упорядочены и требуют относительно мало перестановок.
Очевидно, что этот метод дает упорядоченный массив, и что каждый проход будет использовать результаты предыдущего прохода, поскольку каждая i-сортировка объединяет две группы, рассортированные предыдущей (2×i)-сортировкой. Также ясно, что приемлема любая последовательность приращений, лишь бы последнее было равно 1, так как в худшем случае вся работа будет выполняться на последнем проходе. Однако менее очевидно, что метод убывающего приращения дает даже лучшие результаты, когда приращения не являются степенями двойки.
Все t приращений обозначим через h1, h2, ..., ht с условиями
ht = 1, hi+1 < hi, i=1, …, t-1.
Каждая h-сортировка программируется как сортировка простыми включениями.
Программа сортировки методом Шелла может иметь следующий вид:
Procedure ShellSort;
Var i, j, k, t, m: integer;
x: TElement;
h: Array [1..20] Of integer;
Begin
t:= Round(Ln(N)/Ln(3))-1;
If t = 0 Then t:= 1;
h[t]:= 1;
For m:= t-1 Downto 1 Do
h[m]:= 3*h[m+1] + 1;
For m:= 1 To t Do Begin
k:= h[m];
For i:= k+1 To N Do Begin
j:= i - k;
While a[j+k-1].Key < a[j-1].Key Do Begin
x:= a[j+k-1];
a[j+k-1]:= a[j-1];
a[j-1]:= x;
j:= j - k;
If j < 1 Then Break;
End {While}
End; {For i}
End; {For m}
End;
В литературе рекомендуется такая последовательность приращений (записанная в обратном порядке):
1, 4, 13, 40, 121,...,
где hi-1= 3hi+1, ht= 1 и t= log3(N-1). Именно такие параметры задаются в подпрограмме ShellSort. Приемлемой считается также последовательность
1, 3, 7, 15, 31,...,
где hi-1= 2hi+1, и t= log2(N-1). Анализ показывает, что в последнем случае затраты, которые требуются для сортировки Nэлементов с помощью алгоритма сортировки Шелла, пропорциональны N 1,2.
11.2.6 Сортировка с помощью бинарного дерева
Метод сортировки простым выбором основан на повторном выборе наименьшего ключа среди Nэлементов, затем среди N-1 элементов и т. д. Понятно, что поиск наименьшего ключа из Nэлементов требует N-1 сравнений, а поиск его среди N-1 элементов - еще N-2 сравнений.
Улучшить сортировку выбором можно в том случае, если получать от каждого прохода больше информации, чем просто указание на один, наименьший элемент. Например, с помощью N/2 сравнений можно определить наименьший ключ из каждой пары. При помощи следующих N/4 сравнений можно выбрать наименьший из каждой пары таких наименьших ключей и т. д. Наконец, при помощи всего N-1 сравнений мы можем построить дерево выбора, как показано на рисунке 11.1, и определить корень, как наименьший ключ.
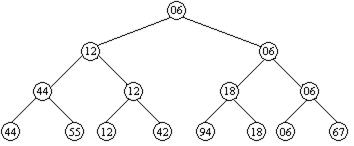
Рисунок 11.1 - Построение дерева при последовательном выборе из двух ключей
На втором шаге выполняется спуск по пути, отмеченном наименьшим ключом, с последовательной заменой его на «дыру» (или ключ-бесконечность). По достижении (при спуске) элемента-листа, соответствующего наименьшему ключу, этот элемент исключается из дерева и помещается в начало некоторого списка. Результат выполнения этого процесса показан на рисунке 11.2.
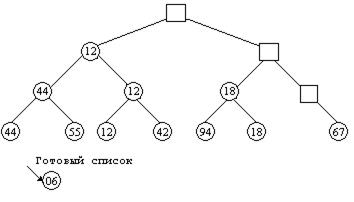
Рисунок 11.2 - Спуск по дереву с образованием дыр и формирование
упорядоченного списка из исключаемых элементов
Затем происходит заполнение элементов-«дыр» в направлении снизу вверх. При этом очередной заполняемый пустой элемент («дыра») получает значение ключа, наименьшего среди значений сыновей этого элемента. В результате получается дерево, изображенное на рисунке 11.3.
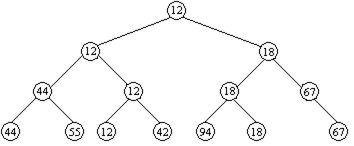
Рисунок 11.3 - Заполнение «дыр»
Элемент, который оказывается в корне дерева, вновь имеет наименьший ключ среди оставшихся элементов и может быть исключен из дерева и включен в «готовую» последовательность. После N таких шагов дерево становится пустым (т. е. состоит из «дыр»), и процесс сортировки завершается.
При сортировке с помощью дерева задача хранения информации стала сложнее и поэтому увеличилась сложность отдельных шагов; в конечном счете, для хранения возросшего объема информации нужно строить некую древовидную структуру. Также желательно избавиться от необходимости в «дырах», которые в конце заполняют дерево и приводят к большому числу ненужных сравнений. Кроме того, нужно найти способ представить дерево из Nэлементов в N единицах памяти вместо 2N-1 единиц. Это можно осуществить с помощью метода, который его изобретатель Дж. Уильямс назвал пирамидальной сортировкой.
11.2.7 Пирамидальная сортировка
Пирамида определяется как некоторая последовательность ключей
K[L], …, K[R],
такая, что
K[i] £ K[2i] & K[i] £ K[2i+1], (11.1)
для всякого i = L, …, R/2. Если имеется массив K[1], K[2], …, K[R], который индексируется от 1, то этот массив можно представить в виде двоичного дерева. Пример такого представления при R=10 показан на рисунке 11.4.
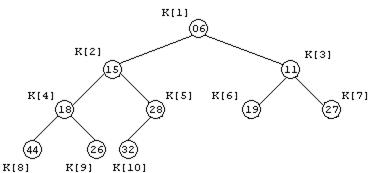
Рисунок 11.4 - Массив ключей, представленный в виде двоичного дерева
Дерево, изображенное на рисунке 11.4, представляет собой пирамиду, поскольку для каждого i = 1, 2, …, R/2 выполняется условие (11.1). Очевидно, последовательность элементов с индексами i = R/2+1, R/2+2, …, R (листьев двоичного дерева), является пирамидой, поскольку для этих индексов в пирамиде нет сыновей.
Способ построения пирамиды «на том же месте» был предложен Р. Флойдом. В нем используется процедура просеивания (sift), которуюрассмотрим на следующем примере.
Предположим, что дана пирамида с элементами K[3], K[4], …, K[10] нужно добавить новый элемент K[2] для того, чтобы сформировать расширенную пирамиду K[2], K[3], K[4], …, K[10]. Возьмем, например, исходную пирамиду K[3], …, K[10], показанную на рисунке 11.5, и расширим эту пирамиду «влево», добавив элемент K[2]=44.
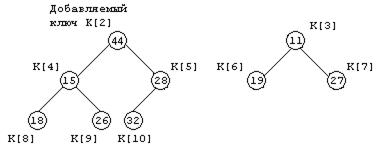
Рисунок 11.5 - Пирамида, в которую добавляется ключ K[2]=44
Добавляемый ключ K[2] просеивается в пирамиду: его значение сравнивается с ключами узлов-сыновей, т. е. со значениями 15 и 28. Если бы оба ключа-сына были больше, чем просеиваемый ключ, то последний остался бы на месте, и просеивание было бы завершено. В нашем случае оба ключа‑сына меньше, чем 44, следовательно, вставляемый ключ меняется местами с наименьшим ключом в этой паре, т. е. с ключом 15. Ключ 44 записывается в элемент K[4], а ключ 15 - в элемент K[2]. Просеивание продолжается, поскольку ключи-сыновья нового элемента K[4] оказываются меньше его - происходит обмен ключей 44 и 18. В результате получаем новую пирамиду, показанную на рисунке 11.6.
В нашем примере получалось так, что оба ключа-сына просеиваемого элемента оказывались меньше его. Это не обязательно: для инициализации обмена достаточно того, чтобы оказался меньше хотя бы один дочерний ключ, с которым и производится обмен.
Просеивание элемента завершается при выполнении любого из двух условий: либо у него не оказывается потомков в пирамиде, либо значение его ключа не превышает значений ключей обоих сыновей.
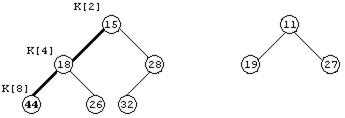
Рисунок 11.6 - Просеивание ключа 44 в пирамиду
Алгоритм просеивания в пирамиду допускает рекурсивную формулировку:
1) просеивание элемента с индексом temp,
2) при выполнении условий остановки - выход,
3) определение индекса q элемента, с которым выполняется обмен,
4) обмен элементов с индексами temp и q,
5) temp:= q,
6) перейти к п. 1.
Этот алгоритм в применении к нашему массиву а реализован в подпрограмме Sift, которая выполняет просеивания в пирамиду с максимальным индексом R:
Procedure Sift(temp, R: Integer);
Var q: integer;
x: TElement;
Begin
q:=2*temp;
If q > R Then Exit;
If q < R Then
If a[q-1].Key > a[q].Key Then q:= q + 1;
If a[temp-1].Key <= a[q-1].Key Then Exit;
x:= a[temp-1];
a[temp-1]:= a[q-1];
a[q-1]:= x;
temp:= q;
Shift(temp, R);
End;
Процедура Shift учитывает индексацию вектора а от нуля.
Теперь рассмотрим процесс создания пирамиды из массива a[0], a[1], …, a[HighIndex]. Напомним, что элементы этого массива индексируются от 0, а пирамида от 1 и, кроме того, N = HighIndex+1. Ясно, что элементы a[N/2], a[N/2+1], …, a[HighIndex] уже образуют пирамиду, поскольку не существует двух индексов i (i= N/2+1, N/2+2,…) и j, таких, что, j=2i (или j=2i+1). Эти элементы составляют последовательность, которую можно рассматривать как листья соответствующего двоичного дерева. Теперь пирамида расширяется влево: на каждом шаге добавляется новый элемент и при помощи просеивания помещается на соответствующее место. Этот процесс иллюстрируется следующим примером.
Процесс построения пирамиды (жирным шрифтом отмечены ключи, образующие пирамиду на текущем шаге ее построения):

Следовательно, процесс построения пирамиды из N элементов «на том же месте» можно описать следующим образом:
R:= N;
For i:= N Div 2 Downto 1 Do
Sift(i, R);
Для того, чтобы получить не только частичную, но и полную упорядоченность элементов нужно проделать Nсдвигающих шагов, причем после каждого шага на вершину дерева выталкивается очередной (наименьший элемент). Возникает вопрос, где хранить «всплывающие» верхние элементы? Существует такой выход: каждый раз брать последнюю компоненту пирамиды (скажем, это будет х), прятать верхний элемент на место х, а х посылать в начало пирамиды в качестве элемента a[0] и просеивать его в нужное место. В следующей таблице приводятся необходимые в этом случае шаги:
Пример преобразования пирамиды в упорядоченную последовательность
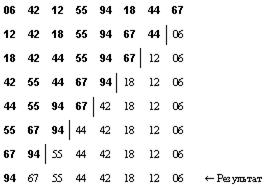
Этот процесс описывается с помощью процедуры Sift следующим образом:
For R:= HighIndex Downto 1 Do Begin
x:=a[0]; a[0]:= a[R]; a[R]:= x;
Sift(1, R);
End;
Из примера сортировки видно, что на самом деле в результате мы получаем последовательность в обратном порядке. Но это легко можно исправить, изменив направление отношения порядка в процедуре Sift (в третьем и четвертом операторах If текста процедуры Sift, приведенного выше). В результате получаем следующую процедуру PyramidSort, учитывающую специфику индексации вектора a:
Procedure PyramidSort;
Var R, i,: integer;
x: TElement;
Begin
R:= N;
For i:= N Div 2 Downto 1 Do
Sift(i, R);
For R:= HighIndex Downto 1 Do Begin
x:=a[0]; a[0]:= a[R]; a[R]:= x;
Sift(1, R);
End;
С первого взгляда неочевидно, что этот метод сортировки дает хорошие результаты. Ведь элементы с большими ключами вначале просеиваются влево, прежде чем, наконец, окажутся справа. Действительно, эта процедура не рекомендуется для небольшого числа элементов, как, скажем, в нашем примере. Однако для больших значений N пирамидальная сортировка оказывается очень эффективной, и чем больше N, тем эффективнее.
Пирамидальная сортировка требует N×log2N шагов даже в худшем случае. Такие отличные характеристики для худшего случая - одно из самых выгодных качеств пирамидальной сортировки.
Но в принципе для пирамидальной сортировки, видимо, больше всего подходят случаи, когда элементы более или менее рассортированы в обратном порядке, т. е. для нее характерно неестественное поведение. Очевидно, что при обратном порядке фаза построения пирамиды не требует никаких пересылок.
11.2.8 Быстрая сортировка разделением
Этот метод основан на принципе обмена. К. Хоар, создатель метода, окрестил его быстрой сортировкой (QuickSort).
Быстрая сортировка основана на том факте, что для достижения наибольшей эффективности желательно производить обмены элементов на больших расстояниях. Реализуется она на основе следующего алгоритма: выбирается любой произвольный элемент массива, называемый медианой далее массив просматривается слева направо до тех пор, пока не будет найден элемент c ключом, большим ключа медианы, допустим это элемент a[i]. Затем массив просматривается справа налево, пока не будет найден элемент a[j], ключ которого меньше ключа медианы. Найденные элементы a[i] и a[j] меняются местами. Затем продолжается процесс «просмотра с обменом», пока два просмотра не встретятся где-то в середине массива. В результате массив разделится на две части: левую - с ключами меньшими медианы; и правую - с большими ключами.
Обычно в качестве медианы выбирается срединный элемент. Если, например, выбрать средний ключ, равный 42, из массива ключей
44, 55, 12, 42, 94, 06, 18, 67,
то для того, чтобы разделить массив, потребуются два обмена:

Конечные значения индексов i=5 и j=3. Ключи a[0], ..., a[i-2] меньше или равны ключу x=42, ключи a[j], ..., a[HighIndex] больше или равны x. Следовательно, мы получили два подмассива
a[k].Кey £ x.Кey для k=0, ..., i-2,
a[k].Кey ³ x.Кey для k=j, ..., HighIndex.
Наша цель - не только разделить исходный массив элементов на большие и меньшие ключи, но также рассортировать его. Однако от разделения до сортировки один шаг: разделив массив нужно сделать то же самое с обеими частями, затем с частями этих частей и т. д., пока каждая часть не будет содержать только один элемент. Этот метод представлен следующей подпрограммой Partition , учитывающей особенности индексации сортируемого массива а:
Procedure Partition(L, R: Integer);
Var i, j: integer;
w, x: TElement;
Begin
If L=R ThenExit;
i:= L; j:= R;
x:= a[(L+R) div 2 - 1];
Repeat
While a[i-1].Key < x.Key Do i:= i+1;
While a[j-1].Key > x.Key Do j:= j-1;
If i <= j Then Begin
w:= a[i-1]; a[i-1]:= a[j-1]; a[j-1]:= w;
i:= i+1; j:= j-1;
End;
Until i > j;
If L < j Then Partition(L, j);
If i < R Then Partition(i, R);
End;
Для запуска процесса сортировки нужно выполнить процедуру QuickSort, которая имеет простую структуру:
Procedure QuickSort;
Begin
Partition(1, N);
End;
Обменная сортировка разделением - самый эффективный из известных методов внутренней сортировки. Это связано с небольшим числом обменов, выполняемых на большие расстояния. Однако быстрая сортировка все же имеет свои «подводные камни». Прежде всего, при небольших значениях N ее эффективность невелика, как и у всех усовершенствованных методов.
Дата добавления: 2015-08-21; просмотров: 1294;
