Поиск, использующий бинарное дерево

Бинарные деревья находят широкое применение для хранения таблицы с тем, чтобы сделать сортировку этой таблицы более эффективной. В этом методе все левосторонние потомки некоторой вершины с ключом Кey имеют ключи, которые меньше ключа Кey, а все правосторонние потомки имеют ключи, которые больше или равны ключу Кey. Смешанный обход такого бинарного дерева дает последовательность, упорядоченную по возрастающему значению ключа. Такое дерево может также быть использовано для бинарного поиска, поэтому оно называется деревом бинарного поиска (binary search tree).

Допустим, имеется следующая последовательность ключей:

30, 47, 85, 95, 115, 130, 138, 159, 166, 184, 206, 212, 219, 224, 237, 258, 296, 307, 314

Дерево бинарного поиска, соответствующего этой последовательности, показано на рисунке 10.3.

Алгоритм поиска в дереве бинарного поиска использует упорядоченность дерева. Поиск элемента выполняется следующим образом. Поиск начинается с корневой вершины, и эта вершина становится текущей. Затем аргумент поиска сравнивается с ключом текущей вершины. Если они равны, то требуемый элемент найден. В противном случае, если аргумент поиска меньше ключа текущей вершины, то выполняется переход к левой дочерней вершине, которая становится текущей. Если аргумент поиска больше ключа текущей вершины, то необходимо перейти к правому сыну текущей вершины, который станет текущей вершиной. В любом случае после перехода к новой вершине происходит этап сравнения ключа с аргументом поиска. Со временем либо определяется нужная вершина, либо достигается лист дерева, что свидетельствует об отсутствии искомого элемента в дереве.

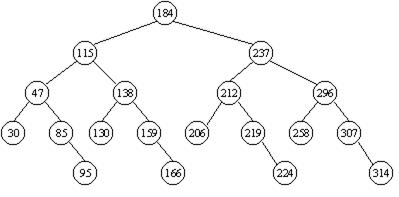
Рисунок 10.3 - Бинарное дерево поиска

Бинарный поиск, рассмотренный ранее, фактически использует отсортированный массив как некоторое неявное дерево бинарного поиска. Срединный элемент этого массива можно представить как корень такого дерева, нижнюю половину массива (все те элементы, которые меньше, чем срединный элемент) можно рассматривать как левое поддерево, а верхнюю половину (все те элементы, которые больше, чем срединный элемент) - как правое поддерево.

Упорядоченный массив может быть получен из дерева бинарного поиска при помощи смешанного обхода этого дерева и вставки каждого элемента последовательно в некоторый массив по мере того, как он встречается в дереве. С другой стороны, для некоторого заданного отсортированного массива имеется много соответствующих ему деревьев бинарного поиска. Предпочтительными являются сбалансированные бинарные деревья, рассмотренные в п. 9.4.2, для которых среднее время, затрачиваемое на поиск, пропорционально log₂N.