Представление полинома Жегалкина в каноническом виде.Представление булевой функции над базисом называется каноническим полиномом (многочленом) Жегалкина.
Алгебра 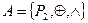 называется алгеброй Жегалкина. Российский математик Жегалкин И.И. (1869-1947) предложил логическую связь, отраженную в таблице 15, называть суммой х и у и обозначать
называется алгеброй Жегалкина. Российский математик Жегалкин И.И. (1869-1947) предложил логическую связь, отраженную в таблице 15, называть суммой х и у и обозначать 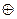 .
.
Таблица 15
| х | у | 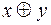
|
В алгебре высказываний сумма истинна тогда и только тогда, когда истинно только одно составляющее сложного высказывания.
Можно также провести аналогию между операцией сложения по mod 2 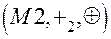 и операцией двоичного сложения. Действительно, 0+0=0
и операцией двоичного сложения. Действительно, 0+0=0
0+1=1
1+0=1
1+1=(1)0, т.е. операция двоичного сложения в пределах последнего двоичного порядка имеет ту же последовательность символов, что и сумма по модулю два. Поэтому операция М2 имеет особое значение в схемах контроля и исправления ошибок. Если один из аргументов из-за неисправности в схеме исказится, то и значение функции изменится на противоположное.
Число полиномов Жегалкина от n переменных составляет 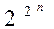 , т.е. равно числу булевых функций от тех же переменных.
, т.е. равно числу булевых функций от тех же переменных.
Теорема (Жегалкин И.И.) Всякая булева функция единственным образом представима в виде полинома Жегалкина.
Единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях.
Представление полинома Жегалкина в каноническом виде выглядит следующим образом:
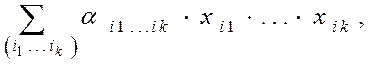
где 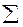 - сложение по модулю два; знак (∙) обозначает конъюнкцию;
- сложение по модулю два; знак (∙) обозначает конъюнкцию; 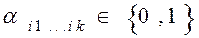
Канонический полином Жегалкина от двух переменных имеет вид:
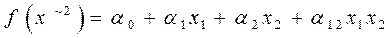
от трех переменных:
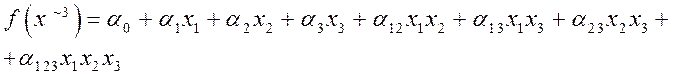 Любой полином Жегалкина может быть приведен к каноническому виду.
Любой полином Жегалкина может быть приведен к каноническому виду.
Пример14. Привести многочлен Жегалкина к каноническому виду.
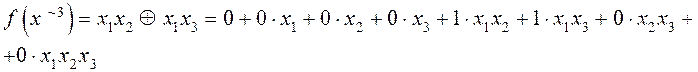 т.е.
т.е. 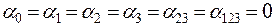
Дата добавления: 2015-08-21; просмотров: 2079;
