К полиному Жегалкина
Указанная выше единственность представления булевой функции полиномом Жегалкина позволяет применять разнообразные методы построения соответствующих данной функции полиномиальных выражений, заботясь лишь о том, чтобы результирующий полином был приведенным, т.е. не содержал одинаковых сомножителей в конъюнкциях и одинаковых слагаемых. Ниже приводятся некоторые из них:
1. Метод, базирующийся на эквивалентном преобразовании формул заключается в следующем:
- представить функцию 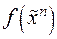 формулой над множеством связок
формулой над множеством связок 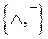 и произвести эквивалентные преобразования, использую соотношения:
и произвести эквивалентные преобразования, использую соотношения:
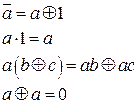
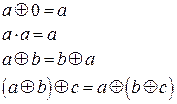
Здесь a, b, c обозначают как переменную, так и формулы.
Пример 15. Привести к полиному Жегалкина функцию 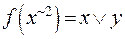
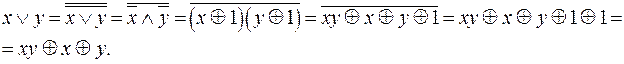
2. Достаточно часто используется метод неопределенных коэффициентов. Рассмотрим его на примере.
Пример 16. Пусть 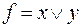 . Использую формулу полинома Жегалкина для двух переменных и придавая х, у возможные значения, выпишем систему уравнений для коэффициентов:
. Использую формулу полинома Жегалкина для двух переменных и придавая х, у возможные значения, выпишем систему уравнений для коэффициентов:
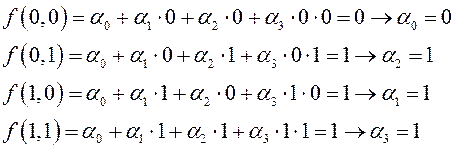
Следовательно, 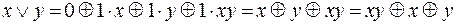 , т.е. мы получим тот же полином Жегалкина, что и в примере 15.
, т.е. мы получим тот же полином Жегалкина, что и в примере 15.
3. Переход от функции, представленной в виде СДНФ, к полиному Жегалкина.
При переходе от булевой функции, представленной в СДНФ, можно заменить знак  на знак
на знак 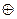 , а
, а 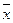 на
на 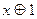 , а затем привести полученное выражение к такому виду, чтобы в нем не было одинаковых сомножителей в конъюнкциях и одинаковых слагаемых.
, а затем привести полученное выражение к такому виду, чтобы в нем не было одинаковых сомножителей в конъюнкциях и одинаковых слагаемых.
Пример 17. Перейти от СДНФ булевой функции 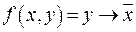 к полиному Жегалкина в каноническом виде.
к полиному Жегалкина в каноническом виде.
1. Построим для 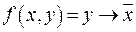 таблицу истинности.
таблицу истинности.
Таблица 16
| х | у | 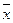
| 
|
2. Найдем СДНФ: 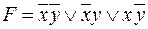
3. Заменив 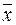 на
на 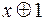 ,
, 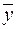 на
на 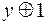 и знак
и знак  на знак
на знак 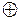 получим:
получим:
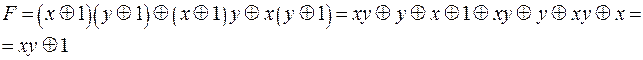
Проверим правильность построения полинома Жегалкина по таблице истинности
Таблица 17
| х | у | ху | 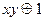
| |
Т.к. итоговые столбцы таблиц 16 и 17 совпадают, то преобразование произведено верно.
Приведем полученный полином Жегалкина к каноническому виду:
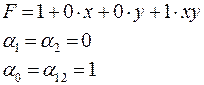
Имеются и другие методы перехода от булевой функции к полиному Жегалкина.
Используя любой из методов перехода можно представить каждую булеву функцию полиномом Жегалкина.
Ниже приведено представление булевых функций от двух переменных полиномами Жегалкина.
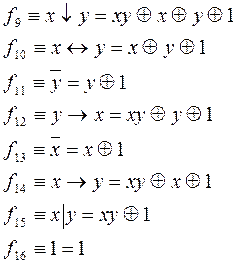
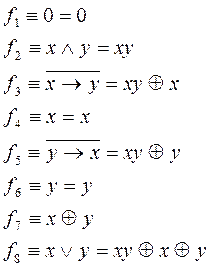
В справедливости вышеприведенных соотношений следует убедиться самостоятельно, используя различные методы перехода от булевой функции к полиному Жегалкина, а затем произвести проверку путем построения таблицы истинности для левой и правой части формул.
Дата добавления: 2015-08-21; просмотров: 3277;
