Специальные представления булевых функций

Дизъюнктивные и конъюнктивные нормальные формы алгебры высказываний.Для каждой функции логики высказываний можно составить таблицу истинности. Обратная задача тоже всегда разрешима. Введем несколько определений.

Элементарными конъюнкциями (конъюнктами) называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более

одного раза.

Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций.

Элементарными дизъюнкциями (дизъюнктами) называются дизъюнкции переменных с отрицаниями или без них.

Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций.

Для каждой функции алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.

Алгоритм построения ДНФ:

1. Перейти к булевым операциям, используя формулы эквивалентных преобразований.

2. Перейти к формулам с тесными отрицаниями, то есть к формуле, в которой отрицания располагаются не выше, чем над переменными – применить законы де Моргана.

3. Раскрыть скобки – применить законы дистрибутивности.

4. Повторяющиеся слагаемые взять по одному разу – закон идемпотентности.

5. Применить законы поглощения и полупоглощения.

Пример 6. Найти ДНФ формулы: .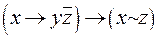

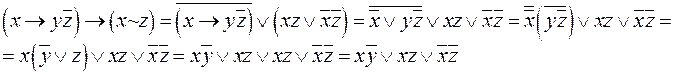
В алгебре Буля справедлив принцип двойственности. Он заключается в следующем.

Функция 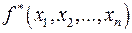называется двойственной к функции 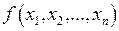, если 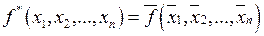. Т.е. для нахождения функции, двойственной к заданной, необходимо построить отрицание функции от отрицаний аргументов.

Пример 7. Найти функцию, двойственную к .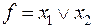

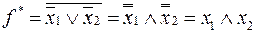
Среди элементарных функций алгебры логики 1 двойственна 0 и наоборот, х двойственна х, 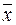двойственна 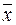, 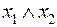двойственна 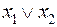и наоборот.

Если в формуле F₁ представляющей функцию 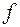все конъюнкции заменить

на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F^*, представляющую функцию 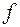^*, двойственную .

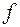Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме: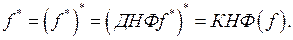

Пример 8. Найти КНФ формулы: .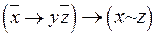

Воспользовавшись результатом примера 6, имеем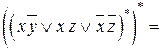

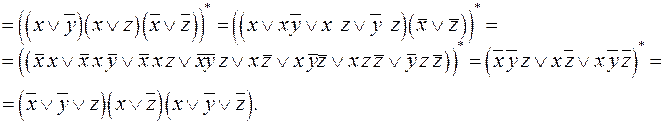
Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы.В каждом из типов нормальных форм (дизъюнктивных и конъюнктивных) можно выделить класс совершенных форм СДНФ и СКНФ.

Совершенной элементарной конъюнкцией называется логическое произведение всех переменных с отрицанием или без них, причем, каждая переменная входит в произведение только один раз.

Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, т.е. добавлением для отсутствующей переменной x_i множится с применением закона дистрибутивности

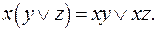
Пример 9. Найти СДНФ для ДНФ примера 6

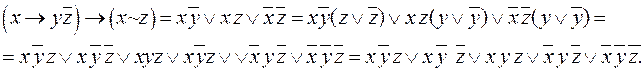
Совершенной элементарной дизъюнкцией называется логическая сумма всех переменных с отрицаниями или без них, причем, каждая переменная входит в сумму только один раз.

Всякую КНФ можно привести к СКНФ, добавляя член конъюнкции, не содержащий какой – либо переменной X_i конъюнкцией 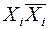и применяя дистрибутивный закон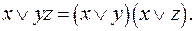

Пример 10 . Привести КНФ к СКНФ: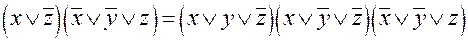

Для построения СКНФ можно воспользоваться схемой

Пример 11. Найти СКНФ для формулы примера 6.

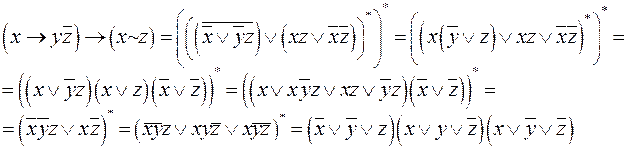
Всякая функция 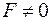имеет СДНФ и, притом, единственную 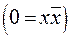. Каждая функция 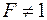имеет СКНФ и, притом, единственную .

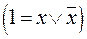Т.к. СДНФ и СКНФ определены формулами однозначно, их можно строить по таблице истинности формулы.

Для построения СДНФ необходимо выделить строки, в которых F принимает значение 1 и записать для них совершенные элементарные конъюнкции. Если значение переменной в нужной строке таблицы истинности равно единице, то в совершенном конъюнкте она берется без отрицания, если нулю – то с отрицанием. Затем совершенные конъюнкты (их число равно числу единиц в таблице) соединяются знаками дизъюнкции.

Для построения СКНФ по таблице истинности необходимо выделить в ней строки, где F=0, и записать совершенные элементарные дизъюнкции, после чего соединить их знаками конъюнкции. Если в требуемой строке таблицы истинности (F=0) значение переменной соответствует нулю, то в совершенном дизъюнкте она берется без отрицания, если единице – то с отрицанием.

Пример 12. Найти СДНФ и СКНФ по таблице истинности для формулы примера 6.

В таблице 14 приведено лишь конечное значение F=10101101. В справедливости этого утверждения следует убедиться самостоятельно, построив развернутую таблицу истинности.

Таблица 14

x	y	z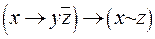

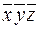
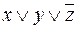
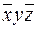
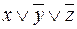
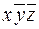
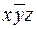
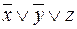
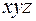
СДНФ =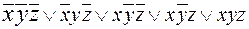

СКНФ = .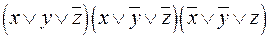

Как видно из примеров 9, 10, 11, 12 значения СДНФ и СКНФ, полученные различными способами, для заданной функции 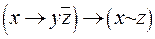совпадают. Это еще раз подчеркивает единственность представления функции в совершенных нормальных формах.