Минимизация нормальных форм
Как было изложено выше, любая булева функция может быть представлена в виде ДНФ и КНФ. Среди этих форм найдутся такие, которые содержат меньшее число переменных, чем исходная.
Дизъюнктивная нормальная форма называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
Одним из способов построения сокращенных ДНФ для функций, зависящих от небольшого числа (не более четырех) переменных, состоит в использовании минимизирующих карт (называемых картами Карно или диаграммами Вейча).
Карта Карно для n переменных служит эффективным средством иллюстративного представления n – куба.
Она содержит 2n ячеек, каждая из которых соответствует одной из 2n возможных комбинаций логических переменных x1, x2, …, xn. Карта строится в виде матрицы размера 2n-k на 2k так, что ее столбцы соответствуют значениям переменных x1, …, xk, строки – значениям переменных xk+1, …, xn, а соседние ячейки (по горизонтали и по вертикалисоседние ячейки соответствуют значениям переменных представления) отличаются только значениями одной переменной. Считается, что каждая клетка таблицы, примыкающая к одной из сторон, является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали.
Нахождение простых импликант сводится к выделению прямоугольников, состоящих из единиц (или х). Для двух переменных карта Карно может иметь вид, изображенный на рис. 3, а для трех переменных – на рис. 4. Для одной и той же функции можно построить несколько карт Карно.
у 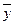
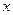
| ||
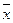
|
Рис.3
у 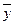
 |
| ||||
| ||||
| ||||
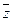
| z | 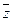
|
Рис.4
Формуле 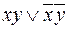 соответствует карта Карно, изображенная на рис.5, а формуле
соответствует карта Карно, изображенная на рис.5, а формуле 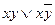 - на рис.6.
- на рис.6.
| у | 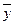
| |
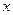
| ||
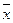
|
| у | 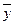
| |
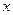
|
 1 1
| |
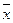
|
Рис.5 Рис.6
Как видно из рис.5, в карте Карно формулы 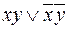 нет элементарных конъюнкций, различающихся по одной переменной. Минимизировать формулу не представляется возможным. Формула
нет элементарных конъюнкций, различающихся по одной переменной. Минимизировать формулу не представляется возможным. Формула 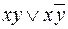 эквивалентна формуле х. Можно проверить аналитически
эквивалентна формуле х. Можно проверить аналитически 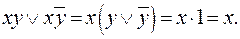
Карта Карно для трех переменных с включенными в прямоугольниках элементарными конъюнкциями приведена на рис.7.
| у | 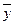
| |||
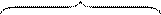 
| ||||
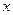
| 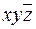
| 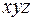
| 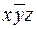
| 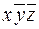
|
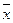
| 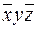
| 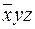
| 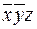
| 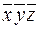
|
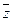
| 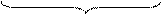
| 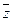
| ||
| z |
Рис.7
Пример 13. Упростить СДНФ формулы 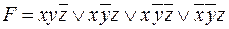 .
.
Данной формуле соответствуют карта Карно, представленная на рис.8.
| у | 
| |||
| ||||
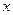
| 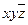
| - | 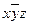
| 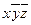
|
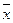
| - | - | 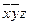
| - |
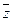
| 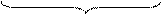
| 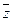
| ||
| z |
Рис.8а. Размещение элементарных конъюнкций формулы F
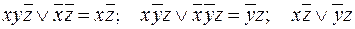
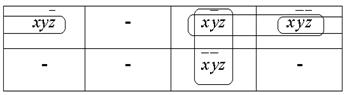
Рис.8б. Первый вариант объединения элементарных конъюнкций формул F
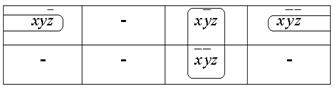
Рис.8в. Второй вариант объединения элементарных конъюнкций формул F
Как видно из рис.8, можно выделить 3 пары элементарных конъюнкций, различающихся по одной переменной. Это 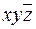 и
и 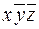 (1 и 4 клетка верхнего ряда),
(1 и 4 клетка верхнего ряда), 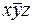 и
и 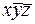 (3 и 4 клетка верхнего ряда),
(3 и 4 клетка верхнего ряда), 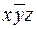 и
и 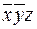 (3-ий столбец).
(3-ий столбец).
Элементарная конъюнкция, записанная в 3-ей клетке верхнего ряда использовано дважды. Это возможно сделать в силу закона идемпотентности.
В результате соответствующие простые импликанты имеют вид для первой пары 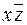 , для второй
, для второй 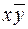 , для третьей -
, для третьей - 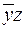 . Таким образом, сокращенная ДНФ будет равна
. Таким образом, сокращенная ДНФ будет равна 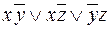 . Как видно из сравнения рисунков 8а и 8в для одной и той же формулы можно построить различные карты Карно. ДНФ, полученная на рис. 8в имеем вид:
. Как видно из сравнения рисунков 8а и 8в для одной и той же формулы можно построить различные карты Карно. ДНФ, полученная на рис. 8в имеем вид: 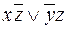 . Она короче, ем ДНФ, построенная на рис. 8б. Обе формулы имеют одну и ту же таблицу истинности (проверить самостоятельно), т.е. эквивалентны, но второй результат предпочтительнее. На картах Карно простой структуры удается непосредственно находить МДНФ (минимальную ДНФ), выбирая те простые импликанты, которые покрывают все единицы и имеют наименьшее возможное число вхождений переменных. В рассмотренном примере это
. Она короче, ем ДНФ, построенная на рис. 8б. Обе формулы имеют одну и ту же таблицу истинности (проверить самостоятельно), т.е. эквивалентны, но второй результат предпочтительнее. На картах Карно простой структуры удается непосредственно находить МДНФ (минимальную ДНФ), выбирая те простые импликанты, которые покрывают все единицы и имеют наименьшее возможное число вхождений переменных. В рассмотренном примере это 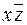 и
и 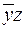 .
.
В силу принципа двойственности всех вышеперечисленных рассуждений вышеизложенный метод может быть применен для нахождения МКНФ. Предварительно следует произвести необходимые преобразования.
Дата добавления: 2015-08-21; просмотров: 1158;
