Минимизация логических устройств

В предыдущей лекции по постановке задачи мы вывели ФАЛ и построили электронную схему, но эта схема будет трудоемкой, неэкономичной и непрактичной, поэтому необходимо минимизировать исходную функцию.

Цель минимизации

1. Уменьшение стоимости

2. Уменьшение числа внешних связей за счет увеличения внутренних

3. Регулярность или упорядоченность внутренней структцры

4. Возможность изготовления полуфабрикатов, то есть возможность решать более сложные задачи

5. Повышение надежности

Способы минимизации

1. Алгебраический метод – упрощение ФАЛ путем использования преобразований алгебры Буля

2. Кубические комплексы

3. Карты Карно

4. Метод Квайна и Мак-Класки

Рассмотрим подробнее каждый из методов

1. Итак мы вывели уравнение:

Используя правила упрощаем его

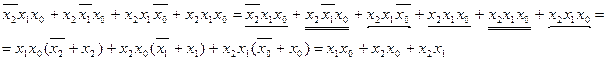
2. Кубические комплексы

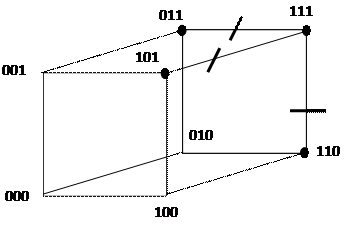Выделяем ребра, которые целиком обозначены существующими в ФАЛ наборами. Записываем соответствующий 0-куб, включающий в себя покрытия ребер, где несовпадающее значение обозначается «_»: ((_,1,1),(1,_,1),(1,1,_)), то есть можно записать .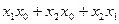

Если точками ограничена вся грань, то она будет описываться только одной переменной, которая совпадает во всех четырех наборах, например передняя грань, полностью описывается переменной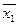

3. Карты Карно

Используются для минимизации Фал, имеющих не более 5 переменных. Карта, это прямоугольная таблица, имеющая 2ⁿ клеток, где n – это количество переменных. Рассмотрим таблицу для 3-х переменных:

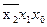
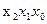
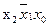
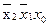
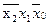
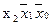
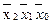
В полученной таблице заменяем существующие в ФАЛ наборы единицами, несуществующие нулями, получаем следующую таблицу:

Записываем пересечения множеств, полностью описывающих прямоугольные выделенные области. То есть получаем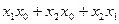

4. Метод Квайна и Мак-Класки используется в автоматизированных системах для упрощения функций.