Минимизация булевых функций

Булевы функции в СДНФ и в СКНФ обычно избыточны. Поэтому этапу построения схемы должно предшествовать упрощение формул или минимизация. Цель минимизации – получить минимально необходимое количество логических элементов в схеме. В основу минимизации положены правила и законы булевой алгебры. Чаще других применяется теорема склеивания:

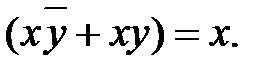
Для применения этой теоремы в функции, представленной в СДНФ отыскиваются слагаемые, отличающиеся только одним аргументом, и склеиваются. Когда все операции склеивания выполнены, можно проверить возможность применения закона поглощения. Для примера проведем минимизацию функции (17.4). Добавим в выражение (17.4) еще два слагаемых 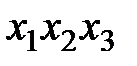. От этого значение функции не изменится (правило 3).

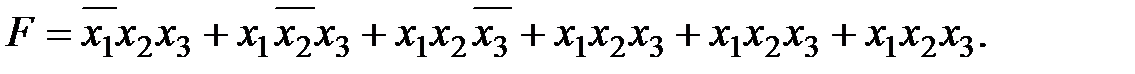
Проведем группирование и возможные склеивания:

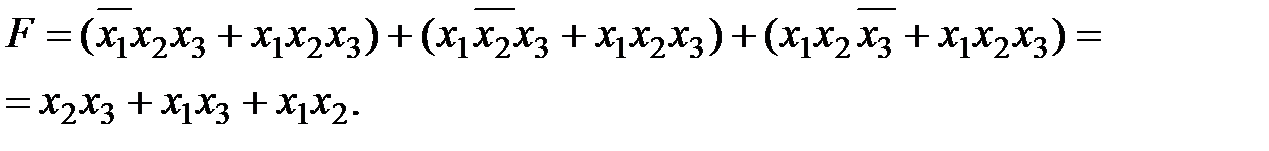(17.6)

Вместо четырех слагаемых третьего ранга (17.4) получили три слагаемых второго ранга. Схема, соответствующая (17.6) приведена на рис. 17.6.

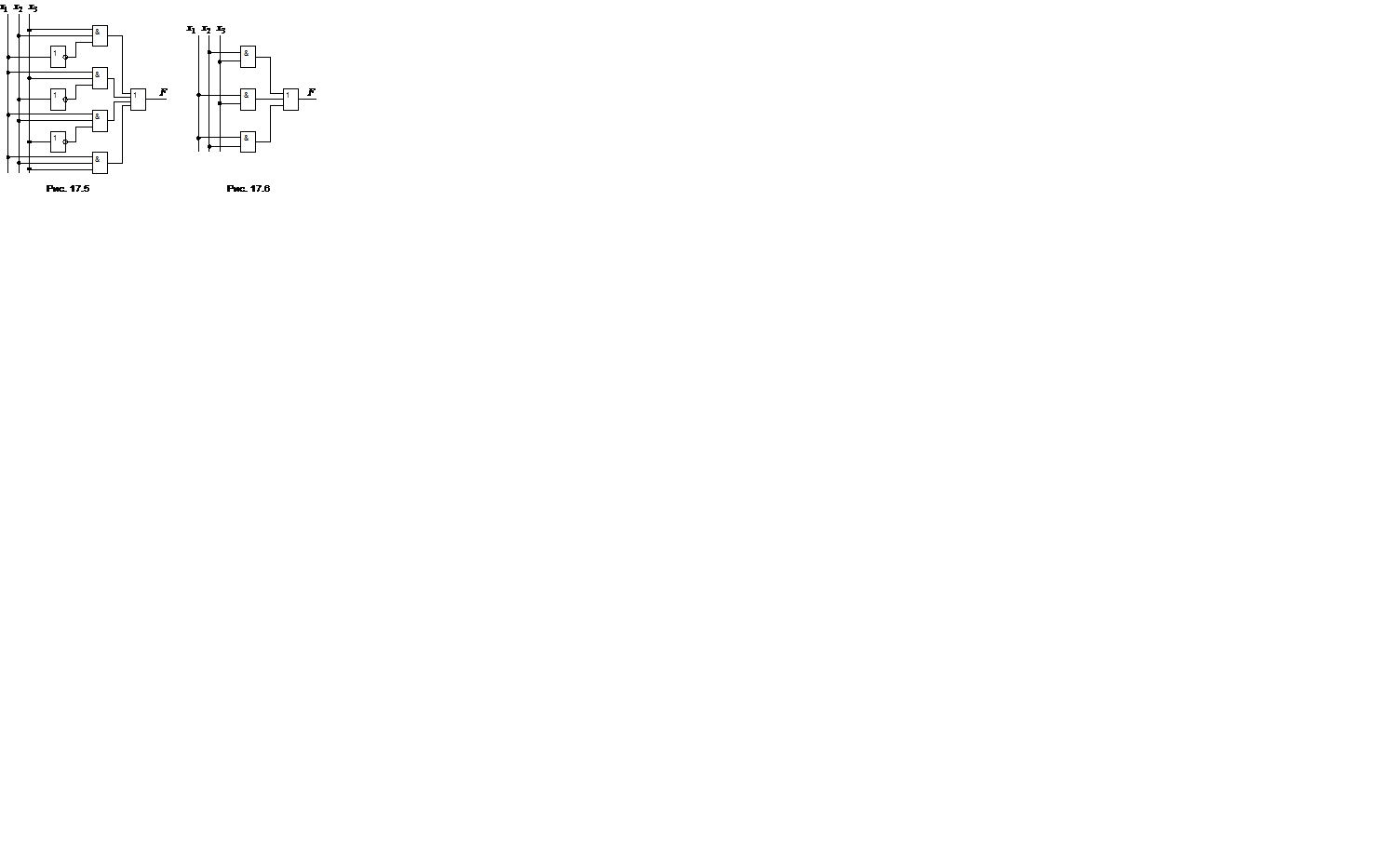
В инженерной практике для минимизации логических функций, как правило, применяют карты (матрицы) Карно. Карта Карно представляет прямоугольник, разбитый на квадраты. Число квадратов равно числу возможных комбинаций, т. е. 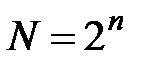. Каждый квадрат соответствует определенной комбинации аргументов (см. рис. 17.7а). Комбинации соседних квадратов должны отличаться не более чем одним аргументом. Для примера на рис.17.7а все возможные комбинации функции 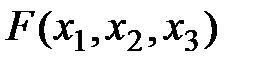Внесены в квадраты карты Карно.

В целях минимизации карта Карно заполняется "1" и "0". Знак "1" записывается в тот квадрат, комбинация которого соответствует значению F = 1. В остальные квадраты записываются "0" (рис. 17.7б). После заполнения

квадраты с "1" объединяют в контуры. Объединить можно 2, 4, 8 квадратов и т. д. Это равносильно объединению слагаемых функции для склеивания. Каждый квадрат может входить в несколько соседних контуров. Возможно объединение крайних квадратов на противоположных сторонах карты.

Объединением двух квадратов исключается один аргумент, четырех квадратов – два аргумента и т. д. В минимизированном выражении функции остаются только те аргументы, значение которых одинаково во всех квадратах контура. Например, для рис. 17.7б результат минимизации будет иметь вид

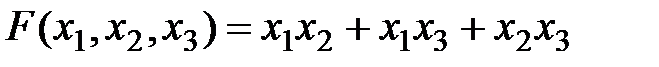
и полностью совпадает с выражением (17.6).