Булевы функции (функции логики).
Результат выполнения логических операций над двоичными переменными называется булевой функцией F. Она может принимать только два значения – "0" или "1". Задать булеву функцию – значит указать ее значение при всех возможных комбинациях переменных (аргументов). Если число переменных равно "n", то число возможных комбинаций равно 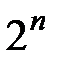 . Когда значение функции известно для всех комбинаций, она называется полностью определенной. В противном случае – частично определенной.
. Когда значение функции известно для всех комбинаций, она называется полностью определенной. В противном случае – частично определенной.
Булевы функции необходимы для синтеза цифровых устройств, содержащих только логические элементы. Для представления булевых функций часто применяют словесное описание, табличное и алгебраическое представление.
Словесное описание функции должно однозначно определять все случаи, в которых выходные сигналы принимают значение "1" или "0". Например: Спроектировать устройство с тремя входами x1, x2, x3, на выходе которого сигнал F = 1 в случае, если на любые два или на все три входа подан сигнал "1".
Табличное представление – это перечисление всех возможных комбинаций входных сигналов. Для устройства, заданного приведенным выше словесным описанием, таблица значений имеет вид
Таблица 17.1
| № п/п | x1 | x2 | x3 | F |
Такая таблица называется таблица истинности.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формул) и для построения логических схем. Существует две формы алгебраических функций – дизъюнктивная и конъюнктивная. Дизъюнктивная нормальная форма представляет собой сумму элементарных произведений аргументов, например
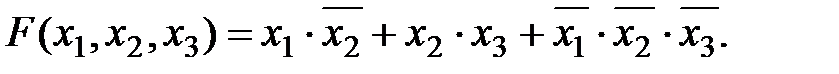
Если каждое слагаемое содержит все аргументы или их отрицания, то получаем совершенную дизъюнктивную нормальную форму (СДФН), например
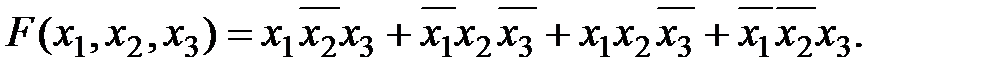
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например
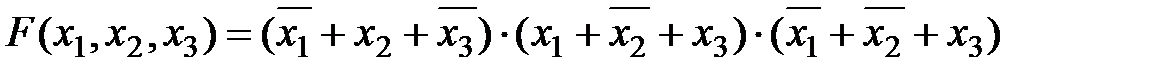
Для перехода от таблицы истинности к СДНФ учитываются только те состояния, для которых функция равна 1. Для каждого такого состояния записывается элементарное произведение всех аргументов. Если аргумент имеет значение "0", то записывается его отрицание. Для приведенного примера СДНФ имеет вид
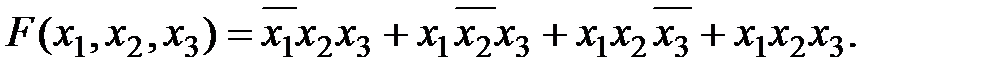 (17.4)
(17.4)
Для перехода от таблицы истинности к СДНФ учитываются только те состояния, для которых функция равна "0". Для каждого такого состояния записывается элементарная сумма аргументов. Если аргумент имеет значение "1", то пишется его отрицание. Для приведенного примера СКНФ имеет вид
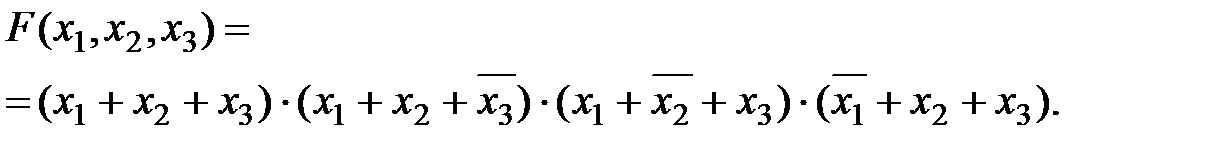 (17.5)
(17.5)
На основании полученных формул (17.4) или (17.5) можно построить логическую схему, состоящую из элементов "ИЛИ", "И", "НЕ". Для функции (17.4) сначала изображаются инверторы, затем ячейки "И" и потом ячейки "ИЛИ" (см. рис. 17.5).
Схемы рис. 17.4 и рис. 17.5 содержат все типы логических элементов. При проектировании всегда стремятся номенклатуру элементов. В связи с этим созданы логические элементы, способные выполнить простейшую функцию двух аргументов "ИЛИ-НЕ", а также "И-НЕ". С помощью каждого из этих элементов можно выразить все основные операции булевой алгебры, а значит реализовать любую логическую функцию. Покажем это.
Для элемента "ИЛИ-НЕ"
операция "НЕ"
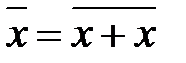
| операция "ИЛИ"
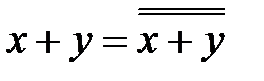
| операция "И"
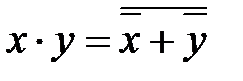
|

Для элемента "И-НЕ"
операция "НЕ"
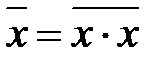
| операция "ИЛИ"
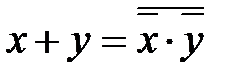
| операция "И"
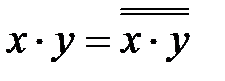
|

В микросхемном исполнении элементы "ИЛИ-НЕ" обозначаются индексами ЛЕ, элементы "И-НЕ" – индексами ЛА. Например, микросхема К555 ЛЕ1 имеет в своем составе четыре элемента "ИЛИ-НЕ" на два входа каждый.
Дата добавления: 2015-08-11; просмотров: 722;
