Граничные условия для нормальных составляющих векторов поля

Установим условия, определяющие поведение нормальных к границе раздела сред составляющих векторов поля. Для этого рассмотрим объем 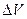(рис. 2а). Обозначим через 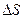поверхность, образованную пересечением 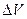с границей раздела сред, а через , 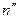— орты нормалей к торцам цилиндра. Считаем, что в каждой точке 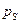существует орт нормали .

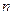Применим третье уравнение Максвелла в интегральной форме к объему 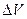, ограниченному поверхностями торцов 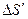, 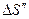и боковой поверхностью цилиндра :

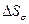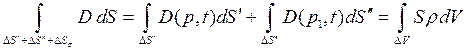(1)

так как при 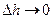имеем 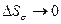и поэтому интеграл по 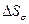стремится к нулю. Учтем, что при , , .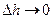

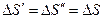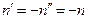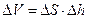Поскольку 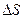мало, то применяя теорему о среднем, можно вынест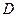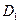и , | и 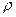из-под знака интеграла. Таким образом, сокращая на 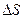, получаем при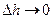

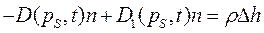(2)

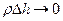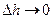На границе раздела S реальных сред заряды не скапливаются, поэтому они не имеют особенности, они не являются поверхностными, т.е. при . Значит,

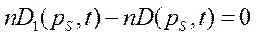(3)

Применим к объему 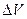четвертое уравнение Максвелла в интегральной форме:

,

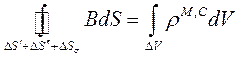где 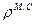- фиктивные сторонние магнитные заряды

При 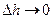имеем

AS'+AS'+AS₆ (4)

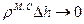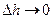Считаем, что на границе раздела реальных сред фиктивный магнитный заряд, как и электрический, не может быть чисто поверхностным, поэтому при . Значит,

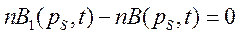(5)

Если 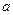— некоторый вектор, то 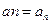— нормальная к S составляющая вектора. Поэтому имеем:

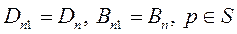(6)

Это математическая формулировка граничных условий для нормальных составляющих векторов индукций: нормальные составляющие векторов индукций при переходе через поверхность раздела реальных сред непрерывны.

Для линейных изотропных сред: , , ,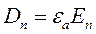

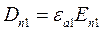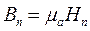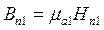
Поэтому в соответствии с (6) нормальные составляющие векторов напряженностей поля имеют скачок на S:

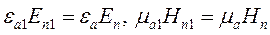(7)