Теорема Винера-Хинчина.
При изучении детерминированных сигналов мы использовали гармони-ческий анализ. Однако в отношении случайных процессов непосредственное использование классического гармонического анализа невозможно, т.к.
1). Реализации случайного процесса xk(t) не удовлетворяют условию аб-солютной интегрируемости 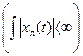
2). Для случайного процесса x(t) частотный спектр также является слу-чайной функцией.
Но можно обобщить гармонический анализ, усредняя спектральные раз-ложения, полученные для отдельных реализаций.
Для этого введем новую функцию 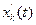 , совпадающую на интервале
, совпадающую на интервале 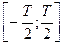 с реализацией xk(t) случайного процесса, а за пределами этого ин-тевала равную нулю:
с реализацией xk(t) случайного процесса, а за пределами этого ин-тевала равную нулю:
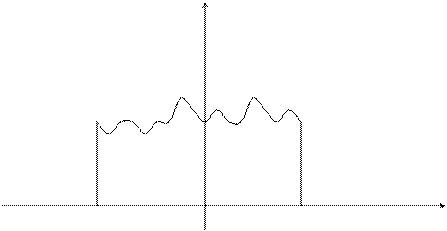 xk(t)
xk(t)
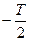 0
0 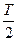
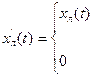 при
при 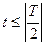
при 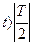
Преобразование Фурье для этой функции:
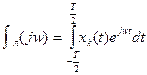
Средняя мощность сигнала 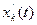
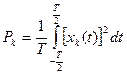
С другой стороны, средняя мощность через частотный спектр:
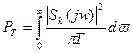
Функция 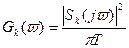 называется спектральной плотностью мощности реализации по спектру частот.
называется спектральной плотностью мощности реализации по спектру частот.
Для определения спектральной плотности совокупности реализаций не-обходимо провести усредненное по ансамблю возможных значений функции 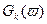
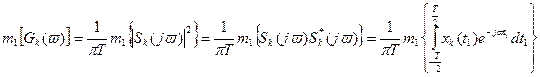
· 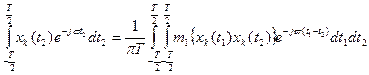
mz – мат. ожидание
kk(t1t2) – корр. Функция
т.к. 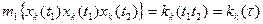
то: 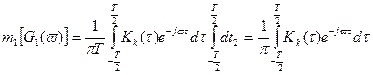
корр. функция выражает связь между значениями случайного процесса в различные моменты времени.
Переходя к пределу при 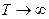 , получим:
, получим:
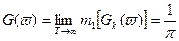
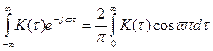
Т.o., спектральная плотность 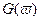 , являющаяся усредненной характери-стикой совокупности реализаций случайного процесса, представляет собой прямое преобразование Фурье для корр. функции.
, являющаяся усредненной характери-стикой совокупности реализаций случайного процесса, представляет собой прямое преобразование Фурье для корр. функции.
Фурье для корр. функции.
Обр. преобр. Фурье:
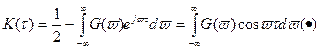
Эти преобразования, связывающие функции 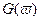 и
и 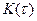 называется преобразованием Хингина-Винера.
называется преобразованием Хингина-Винера.
Если вместо круг. частоты 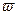 введем частоту в герцах f, то эти выражения примут вид:
введем частоту в герцах f, то эти выражения примут вид:
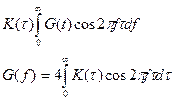
Так как для стационарных эргодических процессов усреднение по множе-ству может быть заменено усреднением по времени, то функция 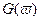 мо-жет быть представлена в виде
мо-жет быть представлена в виде
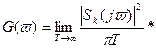
Таким образом энергетический спектр стационарного случайного процес-са может быть вычислен двумя путями:
а) непосредственным наблюдением одной реализации xk(t) и нахождением предела (*).
б) нахождение преобразования Фурье коорр.-ной функции;
Для выяснения физического смысла функции 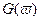 примем в
примем в 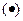
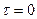 :
:
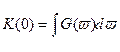
А т.к. К(0) выражает мощность сигнала, то 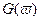 дает усредненную энергетическую картину распределения мощности сигнала по частотному спектру.
дает усредненную энергетическую картину распределения мощности сигнала по частотному спектру. 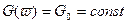
Рассмотрим случай, те есть когда спектральная плотность мощности равномерна на всех частотах спектр называется «белым шумом».
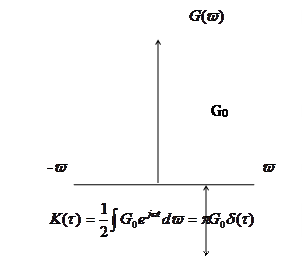 |  | ||||||
 |  |
( 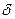 - предел прямоугольного импульса
- предел прямоугольного импульса 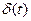 длительности
длительности 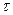 и высота
и высота 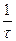 при
при 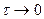 ).
).
Таким образом корр. функция белого шума выражается 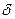 - функцией:
- функцией:
¥ при t=0
K(t) =
0 при t¹0
Белый шум x(t) характеризуется тем, что значения x(t) в любые два момента времени некоррелированы. Такой случайный процесс называется абсолютно случайным.
Белый шум в точном смысле является идеальным, не встречающимся в реальных условиях, потому что:
1). Достаточно близкие значения случайной функции практически всегда зависимы;
2). Реальные процессы имеют конечную мощность, а для белого шума полная мощность процесса бесконечна.
Но: во многих случаях такая идеализация упрощает мат. Анализ и не вносит существенных погрешностей.
Спектры реальных процессов ограничены полосой частот 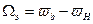 из-за ограниченности полосы пропускания реальных каналов связи.
из-за ограниченности полосы пропускания реальных каналов связи.
Если белый шум пропустить через идеальный фильтр низких частот с граничными частотами 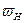 =0,
=0, 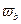 , то на выходе получим шум с ограниченным спектром.
, то на выходе получим шум с ограниченным спектром.
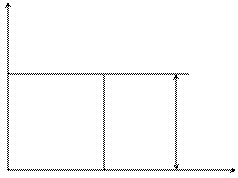 G(
G( 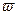 )
)
G0
0 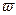
vb
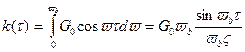 ,
,
где P0=G0vb - средняя мощность процесса
|
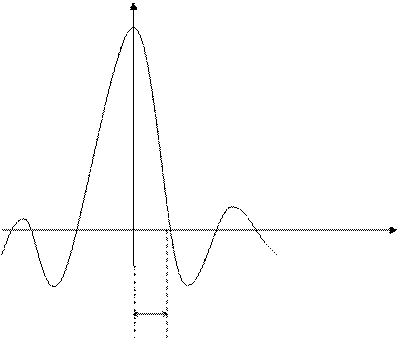 k(t)
k(t)
t
0 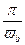
t0
Следовательно, ограничение спектра вызывает появление кореляции, причем по мере сокращения полосы частот Wэ=vb интервал кореляции увеличивается.
В случае, если для случайного процесса спектр непрерывен и сосредоточен около некоторой фиксированной частоты v0, причем выполняется условие
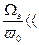 1,
1,
то такой процесс называется узкополосным.
Если узкополосный спектр обладает максимумом при v0 и симметричен относительно этой точки, то коор. Функция процесса
 G(v)
G(v) 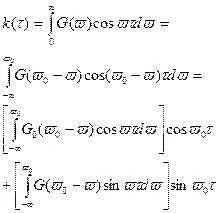
Т.к. по условию полоса спектра пренебрежимо мала по сравнению с частотой v0, то верхние пределы интегрирования могут расп.-ть до ¥.
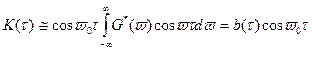
где G*(v)=G(v0-v), 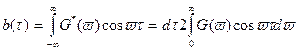
5. Эффективная ширина спектра случайного процесса
При анализе случайных процессов с неравномерным спектром часто пользуются понятием эквивалентной или эффективной ширины спектра, определяемой выражением:
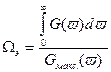 ,
,
где Gмакс.(v) – наибольшее значение функции спектр. плотности;
Средняя мощность процесса:
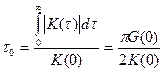 ,
,
то может быть установлена следующая связь между интервалом корреляции и эффективной шириной спектра процесса:
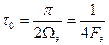
Дата добавления: 2015-08-21; просмотров: 2154;
