Процессы, стационарные в узком смысле слова.

Рассмотрим две системы случайных величин X(t₁), X(t₂),X(t₃),…,X(t_n) и 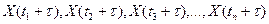. Эти системы соответствуют значениям случайной функции X(t) в моменты t₁, t₂, t₃,….,t_n и .

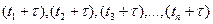Если законы распределения системы случайных величин X(t₁), X(t₂),X(t₃),…,X(t_n) и системы случайных величин 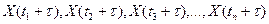совпадают при любых значениях n и выбранных значениях t₁, t₂, ….,t_n и не зависят от 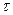, то случайная функция X(t) называется стационарной в узком смысле. Вероятностные характеристикистационарной в узком смысле случайной функции не зависят от абсолютных значений аргумента, а зависят от относительных интервалов между этими значениями.

В дальнейшем, предполагая, что аргументом t случайной функции X(t) является время, мы будем говорить о случайных процессах.

Стационарным в узком смысле случайным процессом называется случайный процесс X(t), для которого n-мерный дифференциальный закон распределения f(x₁, x₂,…x_n; t₁, t₂, …,t_n) зависит при любом t только от интервалов времени между моментами t₁, t₂, ….,t_n..

Так, одномерный дифференциальный закон распределения f(x, t) стационарного в узком смысле процесса не будет зависеть от времени t, двумерный f(x₁, x₂; t_1, t₂) не будет зависеть отдельно от t₁ и t₂, а только от их разностей, например,

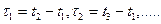
При решении практических задач многомерные дифференциальные законы распределения случайных процессов не рассматриваются. Исследования производят при помощи таких характеристик, как математическое ожидание, дисперсия и корреляционная функция. При этом используется только часть условий стационарности случайных процессов.

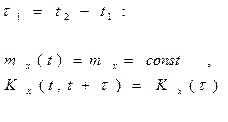(4.192)

Функции, стационарные в широком

смысле, часто называют просто стаци-

онарными.