Как известно, корреляционная функция любой случайной функции

обладает свойством симметрии

(4.193)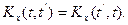

Для стационарного процесса, полагая 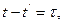получим

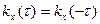, (4.194)

т.е. корреляционная функция 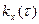-четная функция своего аргумента. Поэтому корреляционную функцию обычно определяют только для положительных значений аргумента (рис. 4.37).

Часто на практике пользуются нормированной корреляционной функцией

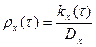(4.195)

где 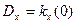- постоянная дисперсия случайного процесса. По существу функция 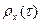представляет собой коэффициент корреляции между сечениями случайной функции, разделенными интервалом 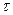во времени. Значение 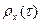в начальной точке 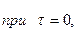очевидно, равно единице

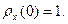
Все эти определения справедливы и в том случае, когда мы имеем дело с функцией многих независимых переменных 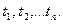В соответствием с этим 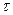может обозначать совокупность разностей 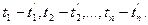Случайную функцию n переменных 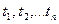называют стационарной в широком смысле, если её математическое ожидание постоянно и корреляционная функция зависит только от разностей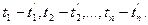

Для стационарных случайных функций – координат точки n- мерного пространства – разработана специальная теолрия, которая в физике называется теорией однородных случайных полей.