Примечание 3

Выражения (1.1.20) и (1.1.21):

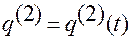
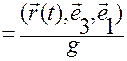, (1.1.20)

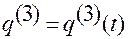
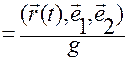(1.1.21)

легко можно записать, зная формулу (1.1.19):

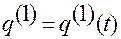
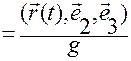, (1.1.19)

Обозначим последовательность индексов у переменных 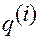, 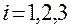в виде

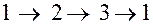(1.1.22)

и последовательность индексов у ортов 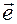также в виде

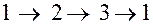. (1.1.23)

Тогда соотношение (1.1.20)

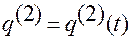
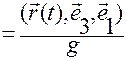, (1.1.20)

получается из (1.1.19)

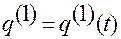
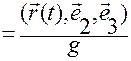, (1.1.19)

заменой в равенстве (1.1.19) индекса «1» при 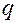на следующий за ним индекс «2» в последовательности (1.1.22)

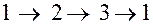, (1.1.22)

и заменой индексов «2» и «3» у ортов 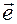на следующие за ними в последовательности (1.1.23)

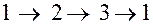(1.1.23)

индексы «3» и «1», соответственно.

После записи выражения (1.1.20) соотношение (1.1.21)

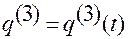
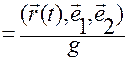. (1.1.21)

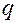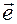строится аналогичным образом из (1.1.20) по правилу замены индексов при и согласно схемам (1.1.22) и (1.1.23).

Если две или более формулы выводятся последовательно друг из друга заменой переменных и (или) индексов на их другие значения из заданных упорядоченных последовательностей, то говорят, что: