Связь векторного и координатного способов
Пусть движениеточки задается координатным способом.
В таком случае формулы (1.1.13) и (1.1.15):
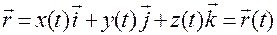 , (1.1.13)
, (1.1.13)
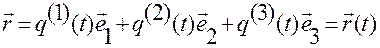 , (1.1.15)
, (1.1.15)
определяют вектор-функцию 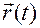 , которая является основой для векторного способа задания движения.
, которая является основой для векторного способа задания движения.
Пусть теперь движениеточки задается векторным способом.
Тогда из (1.1.13) и (1.1.15) можем получить координатный способ задания движения, если вычислим координаты вектор-функции 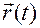 .
.
Будем смотреть на равенства (1.1.13) и(1.1.15) как на уравнения относительно указанных координат. В этих уравнениях известными являются вектор-функции 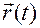 и базисные векторы.
и базисные векторы.
Если системой отсчета является система  , то, умножая (1.1.13) скалярно на
, то, умножая (1.1.13) скалярно на 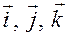 последовательно, получим
последовательно, получим
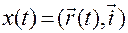 ,
, 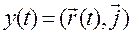 ,
, 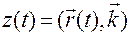 .
.
Здесь
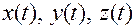 — координаты точки, вычисленные по ее заданному положению
— координаты точки, вычисленные по ее заданному положению 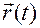 в любой момент времени
в любой момент времени 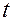 .
.
Как видно из этих выражений, геометрические координаты точки в любой момент времени 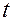 равны ортогональным проекциям вектор-функции
равны ортогональным проекциям вектор-функции 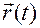 на оси системы отсчета
на оси системы отсчета  в момент времени
в момент времени 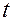 .
.
Аналогично, если система отсчета является аффинной 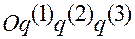 , то, умножая (1.1.15) последовательно скалярно на векторы
, то, умножая (1.1.15) последовательно скалярно на векторы
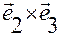 ,
, 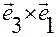 ,
, 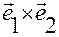 ,
,
получим
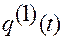
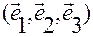
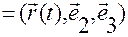 .
.
Отсюда
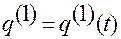
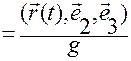 , (1.1.19)
, (1.1.19)
где введено обозначение 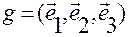 .
.
Дата добавления: 2015-08-21; просмотров: 1470;
