Вычисление координат скорости

Обозначим:

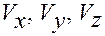— координаты вектора 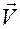в системе отсчета ,

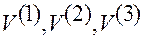— координаты вектора 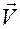в аффинной системе .

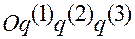По определению координат вектора можем записать

, .

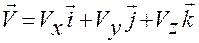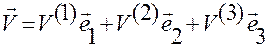Сопоставляя эти соотношения с (1.1.17) и (1.1.18):

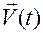
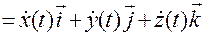; (1.1.17)

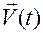
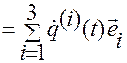. (1.1.18)

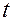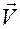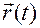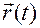видим, что в момент времени координаты скорости совпадают с производными от координат вектора в системе , если движение задается декартовыми координатами, и с производными от координат вектора в системе 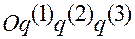, если движение задается аффинными координатами:

, , ;

, , .

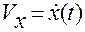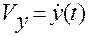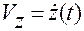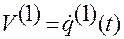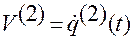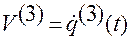Геометрически координаты вектора скорости 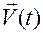можем получить путем совмещения начала вектор-функции 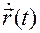с точкой отсчета 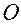и проектирования конца вектора 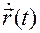на соответствующие координатные оси.