Задание движения точки через координатные функции

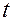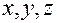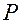Если задать в каждый момент времени координаты точки в виде дважды непрерывно дифференцируемых функций 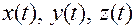, то будем иметь

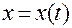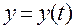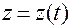, , . (1.1.12)

Тогда, подставляя (1.1.12) в (1.1.10), получим

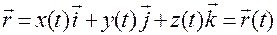. (1.1.13)

Соотношение (1.1.13) позволяет определить положение точки 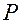в любой момент 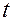из промежутка времени, где заданы правые части равенств (1.1.12).

Причем, поскольку функции 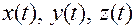дважды непрерывно дифференцируемы, то вектор-функция 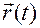, связанная с ними равенством (1.1.13), будет также дважды непрерывно дифференцируема.

А это значит, что соотношения (1.1.12):

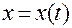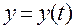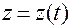, , . (1.1.12)

определяют движение материальной точки.

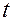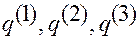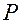Аналогично, задавая в каждый момент времени аффинные координаты точки в виде дважды непрерывно дифференцируемых функций 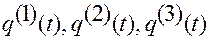, будем иметь

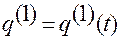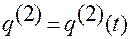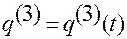, , . (1.1.14)

Подставляя (1.1.14) в (1.1.11):

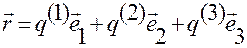, (1.1.11)

получим, что положение 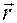точки 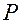в любой момент времени 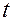может быть вычислено по формуле

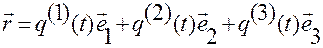. (1.1.15)

Вектор – функция 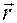, вычисляемая по формуле (1.1.15), определяет движение материальной точки .

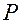В отличие от (1.1.13), по формуле (1.1.15) движение определяется координатными функциями (1.1.14), задающими положение точки в аффинной системе отсчета.