Квантор существования

Квантор существования применяется при частных суждениях.

Выражение "существует по крайней мере один элемент х Î М, обладающий свойством R" обозначают как ( 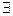x Î M)(R(x)=1).

Знак 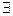называется квантором существования. В качестве символа квантора существования взята перевернутая буква Е (первая буква немецкого слова EXISTIEREN - существовать). В обычной речи слова "некоторый", "несколько" сходны по смыслу с квантором существования.

Квантор существования ставится при частных суждениях, в которых что-либо утверждается или отрицается о части предметов какого-либо класса предметов: "Некоторые металлы плавают на воде".

Если необходимо подчеркнуть, что существует единственный х, такой что R(x), тогда запись принимает такой вид: 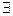!xR(x).

Формула частного утверждения такова: некоторые S суть (или не суть) P .

Частные суждения бывают двух видов:

1. Определенные частные суждения - частное суждение, в котором что-либо утверждается или отрицается только о некоторой определенной части предметов какого-либо класса - "Только некоторые звезды в миллион раз больше нашего солнца". Формула суждения: только некоторые S суть P.

2. Неопределенные частные суждения - частное суждение, в котором что-либо утверждается или отрицается о некоторой части предметов и при этом ничего не утверждается и не отрицается относительно остальных предметов этого класса - "Познакомившись с десятью учениками нового класса, я могу сказать, что некоторые ученики этого класса хорошо знают алгебру". Формула суждения: по крайней мере некоторые С (а может быть и все) суть П.

Квантор существования ( 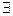x) можно рассматривать как обобщение дизъюнкции, при этом записи ( 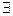x) (F(x)) и F(c1)\/F(c2)\/ . . . \/F(cK) равносильны.

Для бесконечных предметных областей квантор существования играет роль бесконечной дизъюнкции.

Рассмотрим примеры перевода предложений русского языка на язык исчиления предикатов.

"У каждого человека есть отец". Для представления этого педложения неоходимо использовать конструкцию вида "существует такой х , что…" --

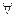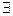х у (человек(х) 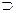отец(у,х)).

Существует решение уравнения (x+1)²=4. Введем предикат равенства =(x, y) и функцию возведения в квадрат kv(z)/

Тогда это высказывание можно записать так

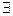x(=(kv(x+1),4)) x=[ –3, 1]