СВЯЗАННЫЕ И СВОБОДНЫЕ ПРЕДМЕТНЫЕ ПЕРЕМЕННЫЕ

Значение предиката (истина или ложь) определяется после подстановки вместо переменных конкретных значений. Например, +(сл1, сл2, сумма):

+(2,3,5) истина +(2,2,5) – ложь.

Мы можем свободно выбирать значения переменных и получать различные значения предиката. Потому такие переменные называют свободными.

Существенным свойством кванторов является то, что они исключают зависимость значения предиката от переменных, превращают свободные переменные в связанные переменные в тех высказываниях, перед которыми стоят кванторы.

Связанная переменная является аналогом индекса в формулах суммирования (произведения) членов ряда или переменной интегрирования в интеграле:

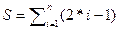
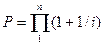
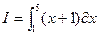
Как известно, значение суммы (произведения) не зависит от индекса, а значение интеграла - от переменной интегрирования. Поэтому всякая формула без свободных переменных (замкнутая формула) является высказыванием, которое истинно или ложно.

Предметная переменная, входящая в формулу, называется свободной, если она не следует непосредственно за квантором и не входит в область действия квантора по этой переменной. Все другие формулы, входящие в формулу, называются связанными.

Областью действия квантора называется та часть формулы, на которую распространяется действие какого-либо квантора. Так в формуле:

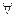x ( x(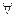P(x)/\Q(x)) /\ P(x)àQ(x))

областью действия квантора 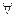х является вся та часть формулы, которая находиться справа от этого квантора (подчеркнуто); областью действия второго квантора 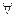x является только, что заключено в первых скобках справа от этого квантора.

Всякая формула со свободными переменными задает некоторое отношение в предметной области, которую иногда называют областью интерпретации.

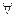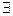Подформула, не содержащая связанную переменную, называют константой относительно квантора х ( х).

Вынесение константы

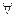x(A(y) & В(х) =А(у) & 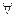х В(х)

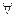x(A(y) V В(х) =А(у) V 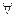х В(х)

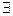x(A(y) & В(х) =А(у) & 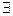х В(х)

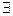x(A(y) V В(х) =А(у) V 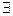х В(х)

Правило переименования (эквивалентности переменных)

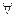x Ф= 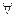y [Ф]_y^x

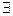х Ф= 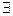у [Ф]_y^x

Запись [Ф]_y^x обозначает результат подстановки терма у вместо всех
свободных вхождений в Ф переменной х.

При подстановке необходимо соблюдать правило – все свободные переменные после подстановок должны остаться свободными.

Рассмотрим пример нарушения этого правила на примере интегрирования:

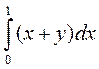Значение интеграла зависит от переменной y. Выполним две подстановки для связанной переменной x

x à z x à y

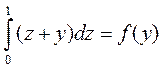
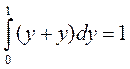
В первом случае формула после подстановки остается правильной, а во втором случае – нет. Это вызвано тем, что переменная y превратилась в связанную переменную.

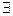х (Øeq(y, x)) - существует х не равный у (своб.перем)

После подстановки у à х получаем логическое выражение

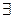у (Ø eq(y, у)) существует у не равный самому себе, что неверно.