ИСЧИСЛЕНИЕ ПРЕДИКАТОВ (ГИЛЬБЕРТА)

К 10 аксиомам, преходящим без изменения из исчисления высказываний, добавляются еще 4.

1. АÉ(ВÉ А)

2. (А É(В É С))É((A É В)É(А É С))

3. (А&В) É А

4. (А&В) É В

5. A É (В É (A & В))

6. A É (B V A)

7. A É (A V B)

8. (A É В) É ((С É В) É ((A V С) É В))

9. (А É В) É ((А É Ø В) É Ø А)

10. Ø Ø A É A

11. 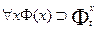Если вместо переменной x поставить конкретный терм, то формула останется истинной. Ф^x_t означает подстановку в формулу терма t: (х, t),

12. 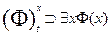Если формула истинна для подстановки (х, t), то можно записать, что существует х, для которых формула истинна.

13. х » х (здесь » символ эквивалентности имен)

14. х » у É ((Ф)_x^z É (Ф)_y^z )

К правилу вывода - исключение импликации (modus ponens - mp)

A, A É B

B

добавляются еще два:

Правило обобщения ® 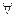x

A É B(х)

A É 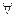x B(Х)

Правило 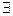x®

В(х) É А

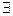x В(х)ÉА

Во втором и третьем правилах В(x) содержит свободное вхождение х, а А их не содержит.

Примеры.

P(x) – предикат: делится на 6;

Q(x) – предикат: делится на 3;

P(x) É Q(x) Из делимости на 6 следует делимость на 3. Это высказывание справедливо для любых х.

Применим правило обобщения

P(x) É 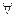x Q(x) Из делимости на 6 следует, что все числа делятся на 3. Это неверно