Интегральное исчисление.
§1. Первообразная. Неопределенный интеграл.
Пусть f(x) – непрерывна на некотором множестве Х.
Опр. Функция F(x) называется первообразной функцией для функции f(x), если ее производная равна исходной функции: 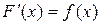 .
.
Например, функция 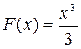 является первообразной для функции
является первообразной для функции 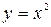 , т.к.
, т.к. 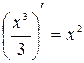 . Заметим, что функция
. Заметим, что функция 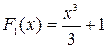 также является первообразной для этой же функции. И вообще, любая функция вида
также является первообразной для этой же функции. И вообще, любая функция вида 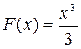 +С (где С – любое число) является первообразной для данной функции
+С (где С – любое число) является первообразной для данной функции 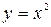 .
.
Теорема. Если 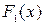 и
и 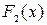 - первообразные для функции
- первообразные для функции  , то найдется такое число С, что
, то найдется такое число С, что 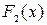 =
= 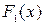 +С.
+С.
Док-во. 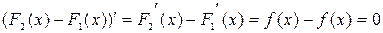 . Тогда
. Тогда 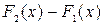 =const =С.▲
=const =С.▲
Таким образом, у всякой непрерывной функции существует бесконечно много первообразных, отличающихся на некоторое число.
Опр. Совокупность первообразных данной непрерывной функции f(x) называется неопределенным интегралом от этой функции и обозначается 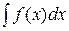 . Таким образом,
. Таким образом,
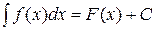 ,
,
где 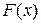 - некоторая первообразная данной функции f(x), С – произвольная постоянная.
- некоторая первообразная данной функции f(x), С – произвольная постоянная.
f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, процесс нахождения НИ – интегрированием или взятием интеграла.
Геометрический смысл первообразной.
Пусть 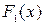 и
и 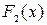 - первообразные для функции
- первообразные для функции  .
. 
Т.к. 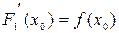 и
и 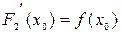 , то касательные к графикам функций
, то касательные к графикам функций 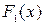 и
и 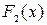 параллельны в любой точке
параллельны в любой точке 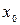 . Таким образом, графики первообразных представляют собой бесконечное семейство параллельных кривых, заполняющих всю плоскость, графики которых можно получить сдвигом на С единиц по оси Оу. Через каждую точку плоскости проходит график одной из первообразных.
. Таким образом, графики первообразных представляют собой бесконечное семейство параллельных кривых, заполняющих всю плоскость, графики которых можно получить сдвигом на С единиц по оси Оу. Через каждую точку плоскости проходит график одной из первообразных.
Дата добавления: 2015-08-14; просмотров: 746;
