Допустимые правила

Доказательство значительно упрощается, если ввести понятие допустимого правила. Допустимое правило представляет собой отрезок готового вывода. Если есть вывод Ф4 Y, то можно вывести правило

Ф

Y

Примеры допустимых правил

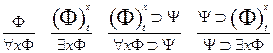
Задача логическая 1

Все люди смертны. Сократ человек. Доказать, что Сократ смертен.

На языке логики эти высказывания запишутся следующим образом.

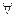х (человек(х) É смертен(х))

человек(Сократ)

---------------------

смертен(Сократ)?

Вывод

1 шаг Подставим вместо переменной х терм Сократ

человек(Сократ) É смертен(Сократ)

2 шаг Выводим по правилу modus ponens

человек(Сократ) É смертен(Сократ), человек(Сократ)

смертен(Сократ)

Вообще можно вывести правило, являющееся аналогом modus ponens, но с квантором всеобщности

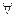х р(х) É q(x), р(а)
q(a)

У любой собаки есть хвост. Полкан - собака. Значит у Полкана есть хвост.

Задача логическая 2

Исходные посылки: все люди смертны. Бог бессмертен. Сократ – человек. Существует ли некто, кто не является Богом.

На языке формальной логики эти фразы запишутся следующим образом.

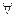x (человек(х) É смертен(х))

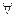x (Бог(х) É Ø смертен(х))

человек(Сократ)

----------------------------------------

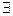х Ø Бог(х)

1 шаг - избавимся от кванторов, подставив вместо связанных переменных термы

человек(t) É смертен(t)

Бог(v) É Ø смертен(v)

человек(Сократ)

2 шаг - подстановка t = Сократ в первую посылку

человек(Сократ) É смертен(Сократ)

3 шаг - из посылки человек(Сократ) и результата второго шага человек(Сократ) É смертен(Сократ) по правилу modus ponens выводим смертен(Сократ)

4 шаг - подстановка v = Сократ во вторую посылку

Бог(Сократ) É Ø смертен(Сократ)

5 шаг - замена импликации

Ø Бог(Сократ) V Øсмертен(Сократ)

6 шаг - по закону коммутативности А V С = С V А

Ø смертен(Сократ) V Ø Бог(Сократ)

7 шаг - возвращаемся к импликации

смертен(Сократ) É Ø Бог(Сократ)

8 шаг из посылки смертен(Сократ) и результата 7 шага

смертен(Сократ) É Ø Бог(Сократ) по правилу modus ponens выводим

Ø Бог(Сократ)

9 шаг - используем квантор существования 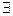х Ø Бог(х)

Вывод сделан. Существует некто, кто не является Богом и этот некто Сократ.