Монотонные функции

Определение. Два набора значений двоичных переменных a=<a₁,a₂,…,a_n> и b=<b₁,b₂,…,b_n> назовём сравнимыми и будем писать
a³ b, если "_i , i=1,…,n a_i ³ b_i. Здесь ³ понимается в обычном виде: 1>0.

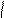
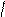Если a³ b и b³ a, наборы считаются несравнимыми.

ПримерПример. Наборы a=<010111> и b=<010101> сравнимы и a³b. Набор a и c=<100111> несравнимы.

Определение. Функция f называется монотонной, если для любых двух наборов значений входных переменных a и b из того, что a³b, следует, что f(a)³f(b).

Свойства монотонных функций.

Нулевой набор значений сравним с любым набором и является меньшим любого из них. Значит, если монотонная функция равна единице на этом наборе, то она равна единице и на любом наборе, т.е. равна константе. Точно так же, если на единичном наборе значений монотонная функция равна нулю, то она не может быть единицей ни на каком наборе, так как единичный набор больше всякого другого набора.

Пусть функция на наборе a, отличном от единичного, равна 1, и пусть значение i-ой компоненты в нём равно 0. Это значит, что на наборе, который отличается только тем, что i-ая переменная в нём равна 1, функция тоже примет единичное значение. Это означает, что конъюнкции в ДНФ, соответствующие этим наборам, можно склеить по переменной xx_i. Точно так же, для набора со значением переменной 0 (т.е. с возможным значением в конъюнкции переменной с инверсией) найдётся набор со значением переменной 1, что приведёт к склеиванию по этой переменной. Следовательно, в минимальной ДНФ монотонной функции нет переменных в инверсной форме.

2.Из этого свойства можно вывести, что суперпозиция монотонных функций снова будет монотонной функцией, т.е. множества монотонных функций образует класс монотонных функций, обозначаемый как M. Базис класса М образуют обе константы и пара функций – конъюнкция и дизъюнкция, т.е. множество {xx×yy, xxÚyy, 0,1}.

Задача. Докажите, что константы должны присутствовать в базисе.

5.6.2. Самодвойственные функции

Определение. Для функции f(xx₁,xx₂,…,xx_n) функция ff(`xx<sub>1</sub>,`xx₂,…,`xx_n) называется двойственной к ней.

Обозначим двойственную функцию как f*.

ПримерПример. Для функции (х×у) двойственной будет функция (`хÚ`у) =xÚy.

Можно показать, что двойственной функцией к f* будет функция f, значит для хÚу двойственной будет х×у.

Двойственной к х будет функция, равная х, двойственной к 0 будет 1.

Определение. Функция называется самодвойственной, если она равна своей двойственной.

Переменная х служит примером самодвойственной функции, так же как и функция инверсии переменной.

Свойства самодвойственных функций.

1. Самодвойственная функция полностью определяется своим видом на верхней половине таблицы истинности. Действительно, если, например, значение функции на наборе <a₁, a₂, …, a_n> равно 0, то значение функции на инверсном наборе <`a<sub>1</sub>,`a₂, …,`a_n> должно быть равно 1.

2. Из первого свойства вытекает, что число различных функций от n переменных равно 2^m, где m=2^n-1.

3. Построим все функции от двух переменных. Их будет 4 в соответствии с возможными значениями на верхней половине таблицы: 00,01,10,11. Эти функции приведены в таблице 5.11. Как видно из таблицы, первые две функции совпадают с переменными, две последние – с инверсиями переменных. Отсюда следует свойство: самодвойственных функций, существенно зависящих ровно от двух переменных нет.

4. СДНФ самодвойственной функции будет иметь ровно 2^n-1 конъюнкций.

5. Суперпозиция самодвойственных функций будет функция самодвойственная. Множество самодвойственных функций образуют класс, который принято обозначать как D. Базисом класса является функция трёх переменных {xx×`yy Úxx×`z Ú`yy×`z}.