Метод неопределенных коэффициентов
Метод может быть применен для минимизации функции любого числа аргументов, однако для простоты изложения и большей наглядности рассмотрим его на примере минимизации функции трех аргументов.
Представим функцию ff(xx1,xx2,xx3) в виде следующей ДНФ:
f(x1,x2,x3=K11x1ÚK10`x1ÚK21x2ÚK20`x2ÚK31x3ÚK30`x3Ú
ÚK1211x1x2ÚK1210x1`x2ÚK1201`x1x2ÚK1200`x1`x2Ú
ÚK1311x1x3ÚK1310x1`x3ÚK1301`x1x3ÚK1300`x1`x3Ú
ÚK2311x2x3ÚK2310x2`x3ÚÚK2301`x2x3ÚK2300`x2`x3Ú
ÚK123111x1x2x3ÚK123110x1x2`x3ÚK123101x1`x2x3Ú
ÚK123100x1`x2`x3ÚK123011`x1x2x3ÚK123010x1`x2x3Ú
ÚK123001`x1`x2x3ÚK123000`x1`x2`x3
Здесь представлены всевозможные конъюнктивные члены, которые могут входить в ДНФ функции f(x1,x2,x3). Коэффициенты K с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого дизъюнктивная форма была минимальной. Если задавать всевозможные наборы значений аргументов <x1, x2, x3> и приравнивать полученное после этого выражение (отбрасывая нулевые конъюнкции) значению функции на выбранных наборах, получим систему 2n уравнений для определения коэффициентов K:
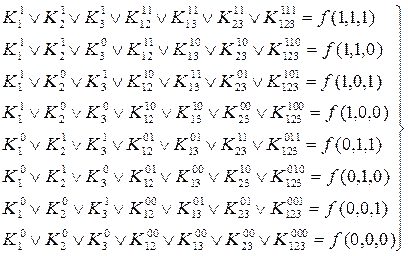
Пусть таблично задана некоторая функция f(x1,x2,x3). Если набор <x1,x2,x3> таков, что функция на этом наборе равна 0, то в правой части соответствующего уравнения будет стоять 0. Для удовлетворения этого уравнения необходимо приравнять 0 все коэффициенты K, входящие в левую часть рассматриваемого уравнения.
В уравнениях, где справа стоят единицы, вычеркнем слева все нулевые коэффициенты. Из оставшихся коэффициентов приравняем единицекоэффициенты, определяющие конъюнкции наименьшего возможного ранга, а остальные примем равными 0 (это можно сделать, так как дизъюнкция обращается в 1, если хотя бы один член ее равен 1). Единичные коэффициенты Ki определят минимальную ДНФ.
ПримерПример 5.f(x1,xx2,x3)=x1xx2xx3Úxx1xx2`x3Úxx1`xx2xx3Úxx1`xx2`xx3Ú`xx1`xx2`xx3.
Составляем систему:
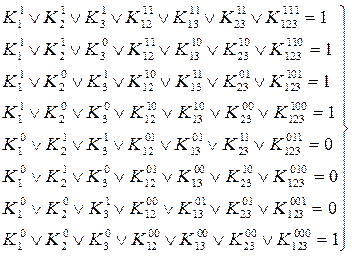
Из пятого, шестого и седьмого уравнений вытекает, что
K10=K20=K21=K30=K31=K1200=K1201=K1300=K1301=K2301=K2310=K2311=K123001=
=K123010=K123011=0.
В результате данная система примет вид
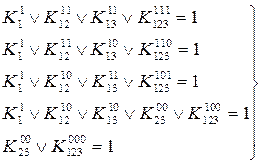
Приравняем 0 в каждом уравнении все коэффициенты, кроме тех, которые отвечают конъюнкциям, содержащим наименьше число переменных:
K1211=K1201=K1311=K1310=K123111=K123110=K123101=K123100=K123000=0.
После этого получаем систему
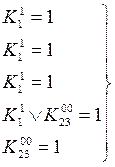
Отсюда находим МДНФ для данной функции: f(x1,x2,x3)=x1Ú`x2`x3.
Описанный метод эффективен лишь для минимизации функций, число аргументов в которых не больше 5-6. Это связано с тем, что число уравнений равно 2n.
Дата добавления: 2015-08-21; просмотров: 862;
