Классы функций алгебры логики

В гл. 4 было введено понятие замкнутого множества, класса, порождающего множества класса и базиса. Рассмотрим эти понятия применительно к множеству ФАЛ.

Над множеством функций F введём операцию суперпозиции функций, состоящую в замене некоторых аргументов одной из fÎF на функции из F. В результате получается новая функция, порождённая суперпозицией. При этом будем считать, что в общем случае аргументы у функций все различны, в частном случае множества аргументов функций могут пересекаться или совпадать. Полученную функцию можно снова использовать в суперпозиции и т.д.

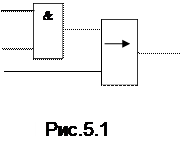
Пример. Пусть F={xx&yy, xx®yy}. Результатом суперпозиции может быть функция х®(yy×z)

Множество всех функций, которые могут быть порождены с помощью суперпозиции из функций множества F, назовём классом функций, порождённых F, и обозначим как ½F½. Множество F называют порождающим множеством класса ½F½

Порождающее множество данного класса называется базисом, если никакое его собственное подмножество данный класс не порождает.

Инженерная трактовка. Сопоставим множеству F множество элементов, реализующих функции из F. Тогда суперпозиции сопоставляется схема из этих элементов, множеству функций класса ½F½–множество всех функций, которые могут быть реализованы такими схемами.

Для рассматриваемого выше примера схема приведена на рис. 5.1.

Рассмотрим основные классы функций алгебры логики.