Осевая теорема Эйлера

Все три рассмотренных выше варианта взаимодействия элементов симметрии составляют суть одной осевой теоремы Эйлера. Взаимодействие двух осей симметрии п-го порядка, поворотных или инверсионных, приводит к возникновению проходящей через точку их пересечения третьей оси симметрии. При этом результирующая ось окажется поворотной, если исходными будут две одинаковые оси (обе поворотные или обе инверсионные), и инверсионной, если исходные оси будут разного типа.

Эту теорему можно сформулировать в общем виде. Произведение двух поворотов вокруг двух пересекающихся осей симметрии эквивалентно повороту вокруг третьей оси, проходящей через точку пересечения первых двух, т.e. два вращения порождают третье, эквивалентное им.

Для доказательства нанесем на поверхность сферы выходы двух пересекающихся в ее центре поворотных осей (рис. 4.8) ~ А и В с элементарными углами поворота α и β соответственно. Результат сочетания двух вращений вокруг указанных осей легко увидеть, рассмотрев движение точки на поверхности сферы (направления вращений указаны стрелками). Для этого на поверхности сферы проведем дуги больших кругов (экваторы) а -а и b -b, полюсами которых служат выходы исходных осей А и В соответственно. Рассмотрим последовательные вращения вокруг указанных осей некоторой точки 1, выбрав ее на поверхности сферы так, чтобы после поворота вокруг оси Л на угол а (движение по экватору а -а) она оказалась на экваторе b -b в положении 2. После поворота точки 2 на угол β вокруг оси В (движение по экватору b -b) она попадет в положение 3. Дуга большого круга, проведенная через точки 1 и 3, является экватором с-с по отношению к полюсу в точке С.

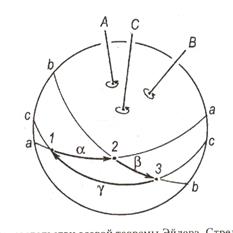
Рис. 4.8. К доказательству осевой теоремы Эйлера. Стрелками показано перемещение точки по экваторам а – а,b –b, с-с при последовательном превращении ее вокруг пересекающихся в центре сферы повторительных осей симметрии А,В,С соответственно

При этом движение точки 1 по экватору с-с в точку 3 можно считать поворотом на угол γ вокруг оси, выходящей в полюсе С. Как видим, два поворота против часовой стрелки вокруг пересекающихся осей А и В можно заменить поворотом в том же направлении вокруг третьей оси С: А_(α) • В_(β) -= С_(γ), , В этом суть известной осевой теоремы Эйлера, лежащей в основе теории симметрии кристаллов. Нетрудно понять, что комбинация вращений вокруг трех пересекающихся осей соответствует операции идентичности, оставляющей точку на месте: А_(α) * В_(β) *С_(-γ)=1