Кристаллах разных сингоний

Пространственная решетка – своеобразный элемент симметрии, за­дающий и осуществляющий повторяемость эквивалентных точек кри­сталлического пространства (в физическом и в геометрическом смысле) в трех некомпланарных направлениях. Решетка как бы управляет рас­положением атомов в кристалле и является тем главным элементом сим­метрии, без которого нельзя представить строение ни одного кристалла.

Решетке подчиняется всякий бесконечный закономерный узор — одномерный, двухмерный, трехмерный. В структуре кристалла беско­нечное число атомов располагается прямолинейными параллельными рядами, в которых (см. рис.5.1) легко прослеживается линейная законо­мерная повторяемость. Обязательной операцией в регулярной бесконечной одномерной постройке служит перенос — трансляция.

Рис.5.1. Узловой ряд

Каждая точка узора при этом преобразовании повторяется в эквивалентных позициях бесчисленное количество раз. Такую же повторяемость можно увидеть и в одномерном узоре — орнаменте (рис.5.2).

Рис. 5.2. Одномерный бесконечный узор — орнамент

Совмещение орнамента с самим собой происходит при переносе – трансляции – этого узора вдоль определенного направления на величину трансляционного вектора 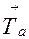. Одномерной «решеткой» такого узора служит узловой ряд — ряд эквива­лентных точек, связанных операцией переноса (рис.5.1). При этом не обязательно, чтобы в узле такого ряда находился атом. В качестве ис­ходной можно взять любую точку одномерного пространства. Тогда в узлах ряда окажутся точки, во всех отношениях эквивалентные исходной. Перемещение фигур при этом может происходить в прямом и обратном направлениях.

Узловые ряды образуют двухмерные узловые сетки, с помощью ко­торых можно описать расположение каких-либо частиц в бесконечном двухмерном узоре (например, в рисунке обоев) (рис.3) или, в част­ности, расположение атомов, ионов, молекул в атомных плоскостях кристаллической структуры.

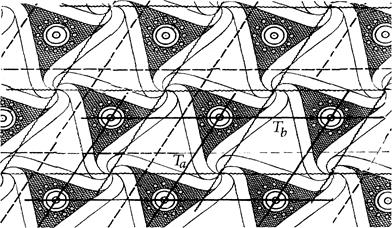
Рис. 5.3. Двухмерный бесконечный узор и его «решетка» — узловая параллелограмматическая сетка. Тип плоской сетки не зависит от того, какая точка принята за исходную.

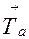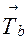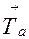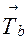Периодичность плоского узора выражает­ся параллелограмматической узловой сеткой — двухмерной решеткой. И любой рисунок обоев или тканей может быть совмещен с самим собой переносом вдоль трансляционных векторов и , лежащих в плоскости рисунка (рис. 5.4.). Минимальным представителем двухмерной ре­шетки является параллелограмм, построенный на двух неколлинеарных векторах и , называемый ячейкой двухмерной решетки. Очевидно, что подобные ячейки заполняют все двухмерное пространство без про­межутков. В трехмерном регулярном узоре, например в кристаллической струк­туре, самосовмещение наступает при переносе вдоль любого трансляци­онного вектора. Периодичность такого узора описывается трехмерной решеткой — параллелепипедальной узловой сеткой, называемой про­странственной решеткой (рис. 5.5). Минимальным представителем трехмерной решетки будет параллелепипед, ребрами которого служат три некомпланарных вектора 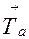, 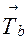и 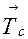— периоды идентичности вдоль трех узловых рядов решетки.

Рис. 5.4. Узловая сетка

Такой параллелепипед повторяемости, или идентичности, называют также ячейкой трехмерной решетки, которая также без остатка заполняет все трехмерное пространство.

Действительно, если в трехмерном пространстве выбрать какую-либо точку (не обязательно материальную) и посчитать ее одним из узлов ре­шетки, то в остальных ее узлах окажутся все точки этого пространства, идентичные (физически и геометрически) исходной. Прикладывая решет­ку к другой заинтересовавшей нас точке при сохранении параллельности решетки самой себе, в ее узлах вновь получим все эквивалентные точки. В результате убеждаемся, что решетка не есть нечто материальное – не конкретная структура кристалла. Т.е. не конкретная укладка атомов (или фигур) в неподвижных узлах решетчатого каркаса, а математический об­раз — схема, с помощью которой мы описываем периодичность кристал­лического вещества, не зависящая от того, какая точка трехмерного про­странства (узора) принята за исходный узел. Иными словами, решетку удобно считать своеобразным элементом симметрии, размножающим точки пространства совершенно аналогично тому, как их размножают другие элементы симметрии — плоскости, оси и т.д. В этом смысле ре­шетка — это свойство кристаллического состояния вещества, ибо любое кристаллическое вещество, даже лишенное каких-либо иных элементов симметрии, всегда обладает этим основным элементом симметрии — ре­шеткой, или решетчатым строением.

Рис. 5.5. Пространственная решетка и ее ячейка