Теоремы сложения элементов симметрии

ТЕОРЕМА 1. Линия пересечения двух плоскостей симметрии является осью симметрии, причем угол поворота вокруг этой оси вдвое больше угла между плоскостями.

ТЕОРЕМА 2. Точка пересечения четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии (центр инверсии)

Зная эту теорему, можно сделать некоторые важные практические выводы: 1)если при исследовании кристаллического многогранника найдены два элемента симметрии из трех (ось симметрии четного порядка, перпендикулярная к ней плоскость, центр инверсий), то обязательно нужно найти недостающий элемент симметрии;2) при наличии центра инверсии количество четных осей симметрии равно числу плоскостей симметрии.

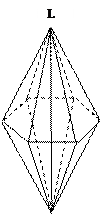
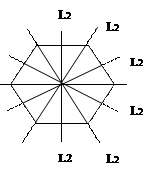
ТЕОРЕМА 3. Если есть ось симметрии порядка «n» и перпендикулярно этой оси проходит ось второго порядка, то всего содержится «n» осей 2го порядка, перпендикулярных оси n-го порядка. Например, в гексагональной дипирамиде, (рис 4.9) шесть осей второго порядка проходят через вершины и середины сторон шестиугольника дипирамиды, а главная ось фигуры L₆ перпендикулярна всем осям второго порядка, и всего есть 6L₂ перпендикулярных L₆.

Рис. 4.9. Положение осей L2 и L6 в дипирамиде

ТЕОРЕМА 4. Если есть ось симметрии n го порядка, и вдоль нее проходит плоскость симметрии, то всего через эту ось будет проходить «n» таких плоскостей.

В самом деле, на данном рисунке видно, вдоль оси L₆ пересекается шесть плоскостей симметрии.

ТЕОРЕМА 5. (выделена впервые русским математиком Леонардом Эйлером, и носит его имя)

Через точку пересечения двух осей симметрии проходит третья ось симметрии. Из рис.4.9 видно, что через точку пересечения двух осей второго порядка действительно проходит третья ось симметрии.