Кристаллографическая символика в гексагональной сингонии
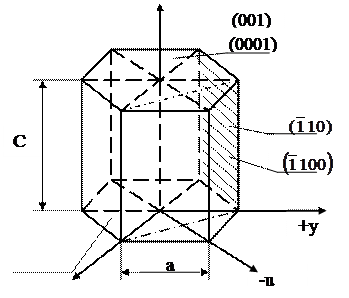
В гексагональной решетке начало координат помещают в центр основания элементарной ячейки (рис. 3.4). Кристаллографические оси х и у проходят из этого центра через вершины шестиугольного основания элементарной ячейки, располагаясь под углом 120° одна к другой, а ось z является вертикальной осью гексагональной призмы. За единицу измерения вдоль осей х и у принимают период решетки а, а вдоль оси z— период с.
В гексагональной решетке, как и в кубической, индексами Миллера плоскости являются приведенные к наименьшим целым числам величины, обратные отрезкам, отсекаемым плоскостью на трех кристаллографических осях. Например, плоскость базиса элементарной ячейки, параллельная осям х и у и отсекающая на оси z отрезок в один период решетки, имеет индексы 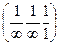 , т.е. (001). Передняя вертикальная грань призмы, отсекающая на оси х отрезок в один период решетки и параллельная осям у и z, имеет индексы
, т.е. (001). Передняя вертикальная грань призмы, отсекающая на оси х отрезок в один период решетки и параллельная осям у и z, имеет индексы 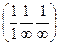 , т.е. (100). Заштрихованная боковая грань призмы, отсекающая на осях х и у отрезки в один период решетки и параллельная оси z, имеет индексы
, т.е. (100). Заштрихованная боковая грань призмы, отсекающая на осях х и у отрезки в один период решетки и параллельная оси z, имеет индексы  , т.е.
, т.е. 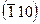 .
.
Рассмотренные плоскости призмы 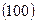 и
и 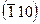 структурно эквивалентны, но они не имеют подобных индексов Миллера. Это неудобно, так как по сочетанию трех индексов нельзя сразу сказать, являются ли непараллельные плоскости (а также направления) структурно эквивалентными. Поэтому чаще пользуются четырехиндексовой системой Миллера—Браве.
структурно эквивалентны, но они не имеют подобных индексов Миллера. Это неудобно, так как по сочетанию трех индексов нельзя сразу сказать, являются ли непараллельные плоскости (а также направления) структурно эквивалентными. Поэтому чаще пользуются четырехиндексовой системой Миллера—Браве.
В плоскости базиса проводят дополнительную ось и, расположенную под углом 120° к осям х и у. Направление - и находится между направлениями + х и + у. Дополнительный индекс i определяют точно так же, как и индексы Миллера, и ставят на третьем месте (hkil).
Положение плоскости в пространстве полностью задается тремя индексами. Поэтому новый индекс является зависимым а именно он равен сумме первых двух с обратным знаком: i= - (h+k). Для проверки правильности написания индексе плоскости индекс i можно не вычислять, а определять одновременно с другими индексами по величине, обратной отрезку, отсекаемому на оси и. Например, передняя вертикальная грань призмы имеет индексы Миллера—Бравэ 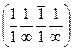 , т.е.
, т.е. 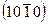 , а боковая заштрихованная грань—индексы
, а боковая заштрихованная грань—индексы 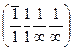 , т.е.
, т.е. 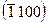 . При четырехиндексовой системе индексы по-разному ориентированных структурно эквивалентных плоскостей получают перестановкой и переменой знака первых трех индексов. Всю совокупность таких плоскостей обозначают заключенными в фигурные скобки индексами любой из плоскостей. Например, структурно эквивалентные плоскости призмы 1-го рода имеют индексы
. При четырехиндексовой системе индексы по-разному ориентированных структурно эквивалентных плоскостей получают перестановкой и переменой знака первых трех индексов. Всю совокупность таких плоскостей обозначают заключенными в фигурные скобки индексами любой из плоскостей. Например, структурно эквивалентные плоскости призмы 1-го рода имеют индексы 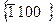 , а плоскости призмы 2-го рода—индексы
, а плоскости призмы 2-го рода—индексы 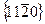 [плоскость с индексами
[плоскость с индексами 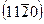 на рис. 10 проходит через штрихпунктирные резки]. Плоскости пирамиды 1-го рода имеют индексы
на рис. 10 проходит через штрихпунктирные резки]. Плоскости пирамиды 1-го рода имеют индексы 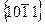 , а 2-го рода
, а 2-го рода 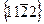 .
.
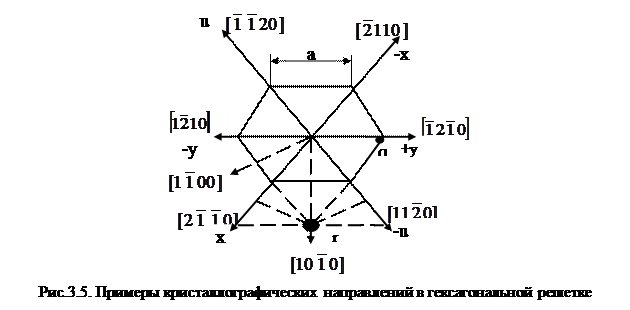
Для определения индексов направлений в гексагональной решетке также чаще используют четырехиндексовую систему. Для этого направление переносят параллельно самому себе в начало координат и из любой его точки опускают перпендикуляры на четыре кристаллографические оси. Например, координатами точки q на (рис. 3.4) по осям х, у, и и z являются отрезки— 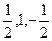 и 0 (ось z перпендикулярна плоскости чертежа). Соответственно направление +у имеет индексы
и 0 (ось z перпендикулярна плоскости чертежа). Соответственно направление +у имеет индексы 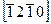 . Шесть структурно эквивалентных направлений +х, —х, +у, —у, +и, —и, имеют индексы
. Шесть структурно эквивалентных направлений +х, —х, +у, —у, +и, —и, имеют индексы 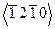 или
или 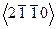 и т.д.
и т.д.
|
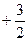 , 0,
, 0, 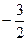 и 0. Направление проходящее через эту точку и начало координат, имеет индексы
и 0. Направление проходящее через эту точку и начало координат, имеет индексы 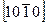 . Соответствующие структурно эквивалентные направления можно обозначить индексами
. Соответствующие структурно эквивалентные направления можно обозначить индексами 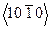 или
или  и т.д.
и т.д.
 | |||
 |
Контрольные вопросы
1. Укажите, какие направления входят в семейство структурно-эквивалентных направлений (как различаются, их индексы для кубической ячейки).
2. Объясните, почему в гексагональной сингонии используют 4-х индексовую систему.
3. Укажите, какие индексы можно менять в семействе структурно-эквивалентных плоскостей в гексагональной ячейке.
4. Объясните, почему третий по порядку индекс плоскости (направления) в гексагональной ячейке можно не писать.
5. Запишите, как можно определить третий индекс плоскости, зная два первых индекса в гексагональной ячейке.
6. Зарисуйте гексагональную ячейку, обозначьте кристаллографические оси, элементарные углы, элементарные трансляции.
7. Запишите, как раскрывают детерминанты уравнения для того, чтобы определить индексы направления по которому пересекаются плоскости с известными индексами.
8. Запишите, как раскрывают детерминанты уравнения для того, чтобы определить индексы плоскости, заключенной между двумя направлениями с известными индексами.
9. Дайте определение оси зоны.
10. Какие грани в кристалле образуют пояс (или зону).
11. Объясните записи: [110], <110>.
12. Объясните записи (110), {110}.
Дата добавления: 2015-08-21; просмотров: 3454;
