Кристаллографическая симметрия

Симметрия (соразмерность) тела представляется как закономерная повторяемость равных его частей, которые могут совмещаться.

О существовании симметрии в природе мы узнаем с раннего детства: симметричны крылья бабочек, стрекоз, лепестки и листья различных цветов и растений, снежинки и т.п. Так, если бабочка сложит крылья, они полностью совместятся. Плоскость, которая разделит бабочку, будет плоскостью симметрии. Если в этой плоскости поместить зеркало, то мы увидим симметричное отражение крыла бабочки. Следовательно, плоскость симметрии обладает свойством зеркальности – по обе стороны от плоскости мы видим симметричные, зеркально-равные половинки тела. В результате изучения кристаллов выяснено, что и в неживой природе, в мире минералов, существует симметрия. В отличие от симметрии в живой природе она называется кристаллической симметрией.

Подкристаллической симметриейпонимается правильная повторяемость элементов ограничения (ребер, граней, углов) и их совмещаемость по определенным направлениям. Наиболее отчетливо симметрию кристаллов обнаруживает их геометрическая форма.

Закономерное повторение геометрических форм можно заметить, если: 1) вращать минерал вокруг определенной оси; 2) рассечь его плоскостью; 3) сопоставить расположение элементов ограничения кристалла относительно точки, лежащей внутри него. Ось, плоскость, точка, расположенные в центре кристалла, называются элементами симметриикристалла.

Осью симметрии называется воображаемая прямая линия внутри многогранника, при вращении вокруг которой на 360º он совмещается несколько раз всеми элементами ограничения с первоначальным положением в пространстве. Ось симметрии обозначается буквой L(рис. 5, б).

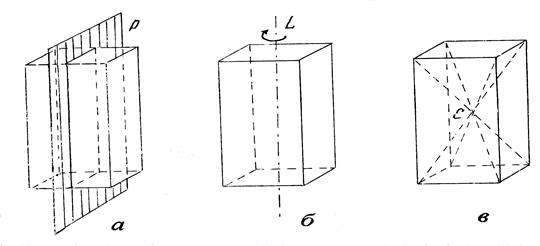
Рис. 5. Элементы симметрии тетрагональной призмы:

а – плоскость симметрии; б – ось симметрии; в – центр симметрии

При вращении кристалла вокруг оси симметрии элементы ограничения будут повторяться определенное количество раз. Число, показывающее, сколько раз кристалл совмещается со своим первоначальным положением в течение полного оборота, называется порядком оси симметрии.Еслимногогранник совмещается дважды, перед нами ось симметрии 2-го порядка, трижды – 3-го порядка.

Выделяются оси симметрии:

L² – 2-го порядка;

L³ – 3-го порядка;

L⁴ – 4-го порядка;

L⁶ – 6-го порядка.

В связи с однородностью кристаллического строения и благодаря закономерностям в распределении материальных частиц внутри кристаллов, доказывается возможность существования в кристаллах только перечисленных выше осей симметрии.

В кристаллических многогранниках может быть несколько осей симметрии различных порядков. Количество осей симметрии того или иного порядка обозначается коэффициентом, который ставится перед символом оси симметрии. Например, куб имеет: 3L⁴, 4L³, 6L²; тетраэдр имеет: 4L³, 3L².

Плоскостью симметриикристалланазывается воображаемая плоскость, которая рассекает его на две равные части, являющиеся одна для другой зеркальным отображением. Плоскость симметрии обозначается буквой Р (рис. 5а). В многограннике может быть несколько плоскостей симметрии. Они обозначаются коэффициентом, который ставится перед буквой Р. Например, куб имеет девять плоскостей симметрии – 9Р, у тетраэдра – 6Р.

Центр симметрии – это воображаемая точка, расположенная внутри кристалла, в которой пересекаются и делятся на две равные части все линии, соединяющие одинаковые элементы ограничения. Центр симметрии (С) в кристалле может быть только один (рис. 5, в).

В результате определения всех элементов симметрии составляется формула для каждого кристаллического многогранника. Например: куб имеет следующие элементы симметрии: 3L⁴4L³6L²9PC; тетраэдр – 4L³3L²6PС.

Задания для самостоятельной работы

1. Найти элементы симметрии в тетраэдре, кубе, октаэдре, тригональной, тетрагональной и гексагональной пирамиде и призме.

2. Написать кристаллографические формулы для каждой модели кристалла.