Элементы симметрии кристаллических многогранников

Как отмечено выше, в кристаллах встречаются симметрично- равные атомные ряды — ряды атомов с одинаковыми периодами, различающиеся лишь своими направлениями в пространстве. Наличие одинаковых межатомных расстояний в таких атомных рядах позволяет мысленно совместить их один с другим либо путем поворота на соответствующий угол, либо путем отражения в зеркальной плоскости. Геометрические образы, указанных преобразований, приводящих к совмещению равных элементов огранки кристаллов или одинаковых атомных рядов или атомных плоскостей, называются элементами симметрии.

Рассмотрим группу элементов симметрии, которые встречаются при описании симметрии кристаллических многогранников.

Простые оси симметрии. Если поворот фигуры вокруг прямой линии, проходящей череп фигуру, на угол 60, 90, 120 или 180° переводит эту фигуру в новое положение, совершенно эквивалентное исходному (когда каждая грань кристалла заменяет равную ей грань, когда каждое ребро кристалла заменяет равное ребро, когда каждая вершина кристалла заменяет равную ей вершину, при этом конечное положение фигуры неотличимо от ее исходного положения), то это является доказательством наличия в кристалле простой оси симметрии соответственно шестого, четвертого, третьего или второго порядков.

Порядок оси симметрии определяется по количеству совмещений фигуры со своим исходным положением за один полный поворот вокруг оси симметрии. Минимальный угол поворота фигуры вокруг оси симметрии, при котором фигура совмещается со своим исходным положением, носит название элементарного угла а. Он связан с порядком оси симметрии n соотношением:

n =360°: а

Разумеется, что в понятие фигуры могут входить не только кристаллические многогранники, ограненные вышеупомянутыми гранями, ребрами, вершинами, но и любая кристаллическая структура с ее атомными рядами и атомными плоскостями. Так, на рис. 4.1 приведен пример плоской атомной сетки, которая содержит простые оси симметрии второго порядка, располагающиеся перпендикулярно этой сетке. Поворот элементарного параллелограмма на 180° вокруг любой из показанных на рисунке осей второго порядка приводит этот параллелограмм к совмещению с исходным положением, либо меняет его местами с другим таким же равным ему параллелограммом. Очевидно, что каждый такой поворот будет приводить к совмещению с исходным положением не только один отдельно взятый элементарный параллелограмм, но вся атомная плоскость при таком повороте займет новое положение, совершенно эквивалентное ее исходному положению, каждый атомный ряд либо совместится со своим исходным положением (поменяв при повороте местами свои концы), либо поменяется местами с равным ему эквивалентным атомным рядом. Наконец, при таком повороте каждый атом займет на плоскости место идентичного атома (либо просто повернется на месте, если он лежит на самой оси симметрии).

Рис. 4.1. Атомная плоскость с простыми осями симметрии второго порядка

Рис. 4.2. Атомная плоскость с простыми осями симметрии третьего порядка

Рис.4.3.Атомная плоскость с простыми осями симметрии четвертого порядка

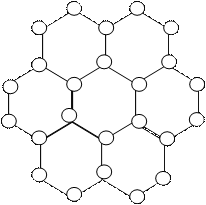Рис.4.4. Атомная плоскость с простыми осями симметрии шестого порядка

Примеры плоских атомных сеток с другими простыми поворотными осями симметрии приведены на рис, 4.2, где оси симметрии третьего порядка проходят перпендикулярно плоскости чертежа через вершины треугольников и их центры, на рис.4.3, где оси симметрии четвертого порядка проходят перпендикулярно атомной плоскости через вершины и центры квадратов, и на рис. 4.4, где оси симметрии шестого порядка проходят через центр каждого правильного шестиугольника — гексагона.

Важной отличительной особенностью всех рассмотренных плоских атомных сеток является то. что они оказываются целиком заполненными одинаковыми правильными фигурами либо параллелограммами, либо правильными равносторонними треугольниками, либо квадратами, либо гексагонами, которые без просветов покрывают всю атомную плоскость. Очень важно отметить, что никакие другие одинаковые правильные многоугольники не могут заполнить плоскость без просветов: ни пятиугольники, ни семиугольники, ни восьмиугольники и т. д. Такое сопоставление доказывает, что в кристаллах могут присутствовать оси симметрии только указанных порядков: второго, третьего, четвертого и шестого.

В проведенном анализе мы не упоминали оси симметрии первого порядка, поскольку этот элемент симметрии имеет тривиальный смысл: любая фигура содержит бесчисленное множество таких осей.

Таблица 4.1