По символам атомных рядов

Пусть атомная плоскость задана с помощью двух принадлежа­щих ей непараллельных друг другу атомных рядов, которые описываются соответствующими символами [u₁v₁w₁] и [u₂v₂w₂]. Подобное определение плоскости эквивалентно заданию плос­кости с помощью трех точек с координатами: [[u₁v₁w₁]], [[u₂v₂w₂]] и [[0; 0; 0]], поскольку две первые точки соответствуют координатам радиусов-векторов и , исходящими из третьей точки - начала координат [[0; 0; 0]].

Запишем уравнение плоскости (hkl) проходящей через на­чало координат: hx+ky+lz=0 и определим искомые индексы плоскости из условий принад­лежности точек [[u₁v₁w₁]] и [[u₂v₂w₂]] этой плоскости:

hu₁+kv₁+lw₁=0; hu₂+kv₂+lw₂=0;

После умножения первого уравнения на w₂, и второго уравне­ния на (-w₁)и их сложения получим отношение индексов h и k, которое выражено через индексы двух заданных направле­ний:

h:k=(v₁ w₂ – v₂ w₁):(w₁ u₂ – w₂ u₁)

Аналогичным образом можем получить отношение для индек­сов k и l:

k:l=(w₁ u₂ – w₂ u₁):(u₁ v₂ – u₂ v₁)

Объединяя оба отношения, получим решение поставленной за­дачи в общем виде:

h:k:l=+-(v₁w₂ – v₂w₁):(w₁u₂ – w₂u₁) :(u₁v₂ – u₂v₁) (3.1)

Для удобства вычисления индексов плоскости по заданным индексам принадлежащих этой плоскости направлений исполь­зуют мнемоническое правило «перекрестного умножения». Для этого каждый из символов направлений записывают по два раза подряд - в строчку так, чтобы в одной строке были ин­дексы одного направления и чтобы одноименные индексы при такой записи оказались в одинаковых столбцах:

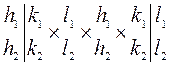
Затем, отбрасывая крайние столбцы и выполняя перемно­жение в соответствии со стрелками, т. е. крест-накрест, полу­чают результат, отвечающий формуле (3.1):

h:k:l=(v₁ w₂ – v₂ w₁):(w₁ u₂ – w₂ u₁) :(u₁ v₂ – u₂ v₁)

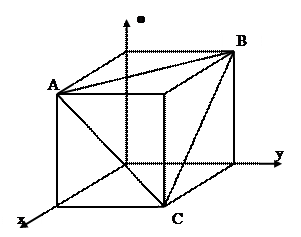
Пользуясь правилом перекрестного умножения, найдем сим­вол атомной плоскости АВС, проходящей через три вершины куба (рис. 3.1), по заданным символам диагоналей его граней ВС 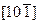и АВ :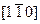

Таким образом, искомый символ плоскости АВС мы опреде­лили с точностью до знака: ±(111), поскольку выбранный по­рядок перемножения символов может быть произвольным.

Отметим важный результат, который можно получить, под­ставляя отношение (3.1) в выра­жение для нормали к плоскости.

При равенстве осевых единиц и взаимной перпендикулярности базисных векторов (т.е. для ку­бических кристаллов, для описа­ния которых применяется при­вычная декартова система координат) выражение для нормали принимает следующий вид:

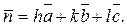
Тогда в соответствии с отношением u:v:w=m:n:p, символ, определяющий направление нормали , принимает вид [hkl], поскольку числа h, k, l являются координатами вектора нормали. Таким обра­зом, в данном случае (и только в данном случае) численные значения индексов плоскости (hkl) и направления ее нормали [uvw] совпадают: h=u, k=v, l=w.

Например, нормаль к плоскости 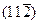кубического кристалла описывается с помощью таких же индексов -

3.2. Определение символа атомной плоскости по координатам трёх

узлов пространственной решётки

Положение атомной плоскости в кристалле наряду с описан­ными методами может быть также определено с помощью сов­мещенных с этой плоскостью трех узлов пространственной ре­шетки.

Пусть заданы координаты трех узлов пространственной ре­шетки.

М₁[[m₁; n₁; p₁]], М₂[[m₂; n₂; p₂]], М₃[[m₃; n₃; p₃]],

Тогда отношение индексов атомной плоскости можно опреде­лить с помощью трех детерминантов:

(3.2)

С помощью формулы (3) определим символ плоскости, заданной тремя точками М₁[[1; 1/2; 1]], М₂[[1/2; 1; 1]], М₃[[1; 1; 1/2]]:

В результате получим символ плоскости (111).

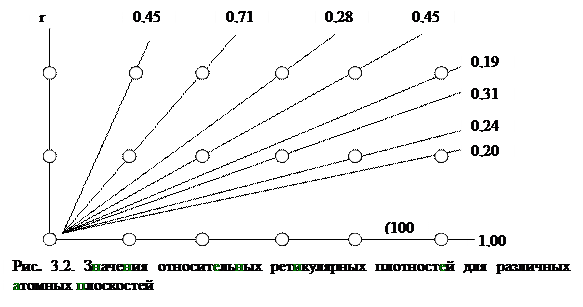
В заключение отметим, что индексы плоскости h, k, l в боль­шинстве случаев выражаются небольшими (однозначными) числами, что непосредственно связано с законом Бравэ. Действительно, наиболее плотноупакованным граням кристалла соответствуют сравнительно высокая ретикулярная плотность, высокая вероятность образования грани на растущем кристалле и небольшие численные значения индексов. Так, с уменьшением ретикулярной плотности r атомных плоскостей увеличиваются значения индексов (рис. 3.2).

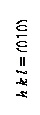3.3. Определение символов граней и направлений по методу

косинусов в кубической решетке

Положение любой грани кристалла (h k l) ( или плоскости в решетке) определяется углами, которые составляют нормаль к этой грани с осями координат. Плоскость АВС отсекает на осях координат отрезки ОА, ОВ, ОС (рис.3.3)

Из начала координат опущен перпендикуляр на плоскость АВС. Нормаль ОР образует с осями координат углы

Из чертежа вытекает, что ; ; .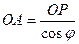

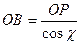Если ОА=m, ОВ=n, OC=p, то .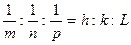

С другой стороны

В результате, для кубических кристаллов 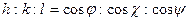, то есть составив отношение направляющих косинусов легко получить символ грани.

Символ направлений связан с направляющими косинусами соотношением , в котором углы между соответствующими кристаллографическими осями и направлением.

Рис. 3.3. К выводу соотношения между индексами и направляющими косинусами грани.