Сведение криволинейного интеграла І рода к интегралу Римана

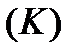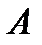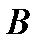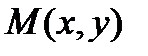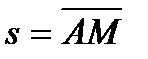Пусть на кривой выбрано направление от до (одно из двух возможных). Тогда положение произвольной точки на кривой может быть определено не только ее координатами , а и длиной дуги , которая отсчитывается от начальной точки 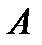. Тогда кривая 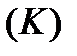может быть параметрически определена следующим образом:

,

где 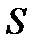- длина всей кривой 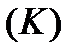. Функция 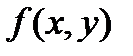, которая определена вдоль кривой 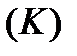, сведется к сложной функции 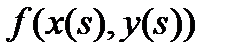от переменной .

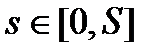Обозначим значения длин дуг, которые отвечают на кривой 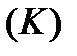точкам 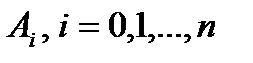, через 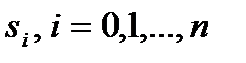, тогда

.

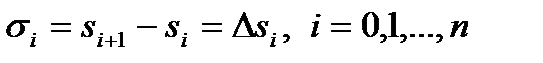Обозначим через 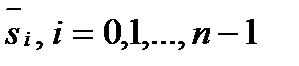, значения длины дуги, которые определяют положение точек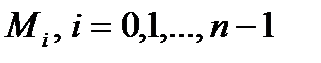 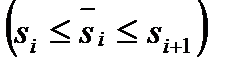. Тогда

,

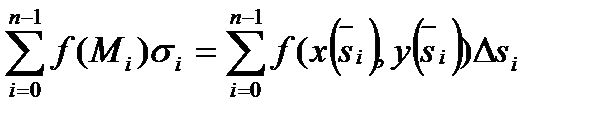т.е. интегральная сумма для криволинейного интеграла І рода является одновременно интегральной суммой для обычного определенного интеграла Римана, поэтому имеем:

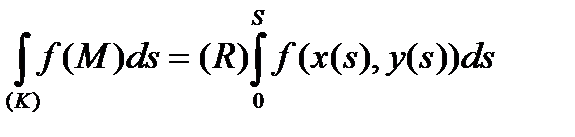, (40)

(где 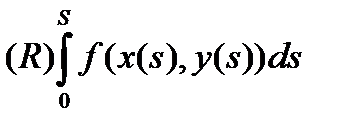означает обычный интеграл Римана), и вдобавок существование одного интеграла влечет за собой существование другого.

Будем дальше предполагать, что функция 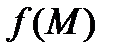, которая определена на кривой 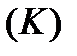, является непрерывной. Пусть теперь простая кривая 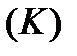определена произвольными параметрическими уравнениями:

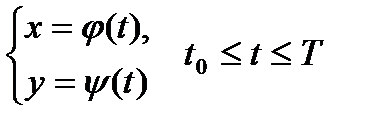, (45)

где функции 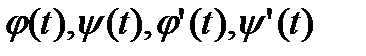- непрерывны. Тогда кривая 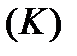является спрямляемой и, если возрастание дуги 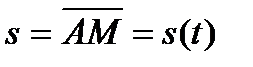отвечает росту параметра 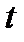, то (как известно из темы «Применение интеграла Римана») длина дуги вычисляется как

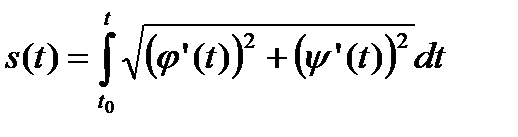. (50)

Тогда

Таким образом, в случае, когда кривая 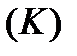определена параметрически с помощью (45), формула сведения криволинейного интеграла І рода к интегралу Римана имеет вид:

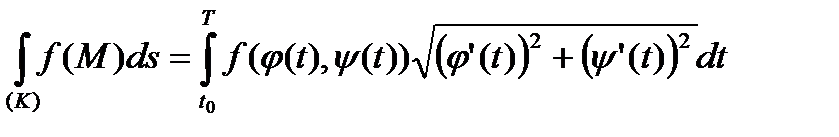. (60)

Пусть теперь кривая 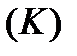определена при помощи обычного уравнения:

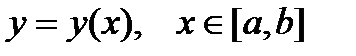, (70)

тогда для того, чтобы применить формулу (60) в этом случае, приведем задание кривой (70) к параметрическому виду обычным способом, рассматривая переменную 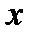как параметр:

.

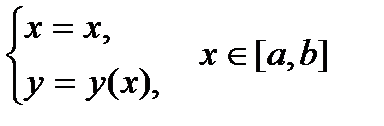Формула (60) принимает вид:

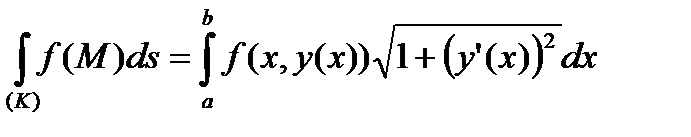. (80)

Пример. Вычислить криволинейный интеграл І рода 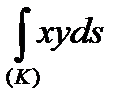, где 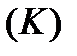- это четверть эллипса , которая находится в І квадранте.

Перейдем к параметрическому заданию нужной части эллипса:

.

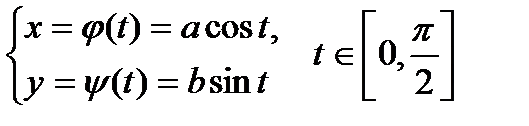Тогда

.

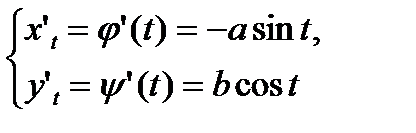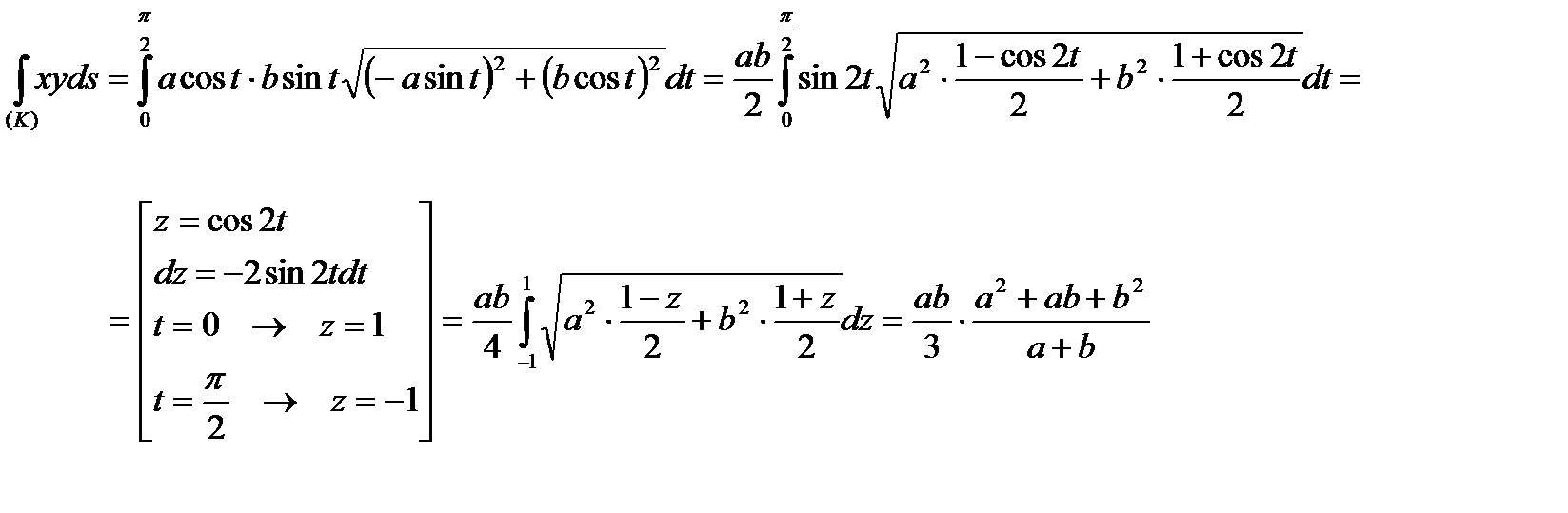
Вопросы

1. Построение интегральной суммы для криволинейного интеграла І рода.
2. Определение криволинейного интеграла І рода.
3. Формула сведения криволинейного интеграла І рода к интегралу Римана в случае, когда кривая определена параметрически.
4. Формула сведения криволинейного интеграла І рода к интегралу Римана в случае, когда кривая определена обычным способом.