Задача о вычислении массы кривой

Лекция 41. Криволинейные интегралы І рода

План

1. Задача о вычислении массы кривой
2. Определение криволинейного интеграла І рода
3. Сведение криволинейного интеграла І рода к интегралу Римана

Задача о вычислении массы кривой

Пусть на плоскости задана непрерывная простая спрямляемая кривая 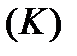некоторой массы (рис.1), известна функция ее линейной плотности 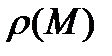во всех точках 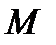кривой. Необходимо определить массу 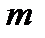всей кривой .

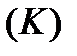Разобьем кривую 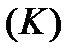на части произвольно выбранными на ней точками 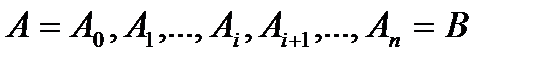(рис.1). Для определенности будем считать, что точки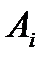

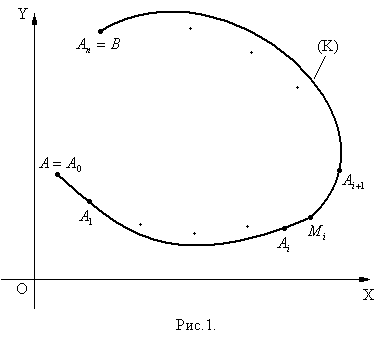
Занумерованы в направлении от 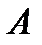до 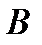(можно и наоборот). На каждой частичной дуге выберем произвольно точку 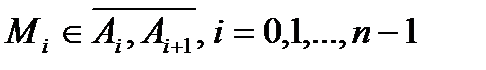, с координатами 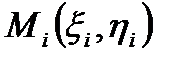(рис.1). Вычислим в точках 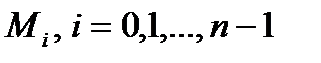, значения 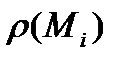. Будем считать, что в каждой точке частичной дуги 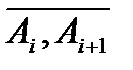такая же плотность. Обозначим 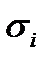длину дуги 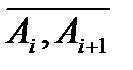. Тогда масса 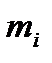частичной дуги 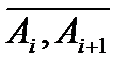будет оцениваться как

,

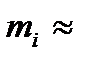
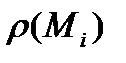
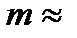
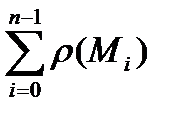
а 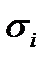. (10)

Если все 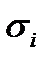стремятся к 0, то погрешность для 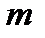, которая вычисляется при помощи формулы (10), тоже стремится к 0.

Пусть

,

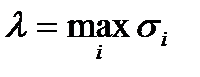тогда

. (20)

Рассмотренная задача дает предварительное наглядное представление о криволинейном интеграле І рода.