Определение криволинейного интеграла І рода
Пусть вдоль кривой 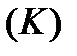 определена некоторая функция
определена некоторая функция 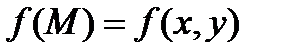 , которую назовем «функцией точки». Повторим действия, проведенные више для задачи о массе кривой для произвольной функции
, которую назовем «функцией точки». Повторим действия, проведенные више для задачи о массе кривой для произвольной функции 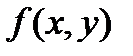 . Пусть
. Пусть 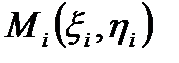
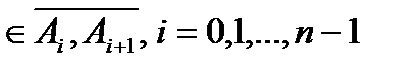 , построим
, построим
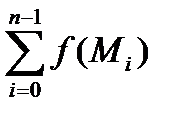
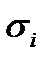 =
= 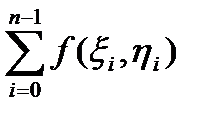
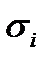 . (30)
. (30)
Сумма (30) является интегральной суммой для криволинейного интеграла І рода.
Аналогичный процесс построения интегральной суммы можно использовать и в случае замкнутой кривой.
Определение 1. Пусть существует конечный предел
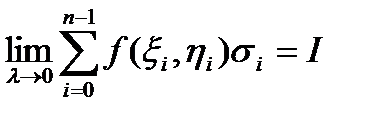 ,
,
который не зависит ни от способа разбиения 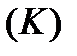 на части
на части 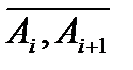 , ни от выбора промежуточных точок
, ни от выбора промежуточных точок 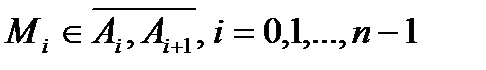 , тогда этот предел называется криволинейным интегралом І рода от функции
, тогда этот предел называется криволинейным интегралом І рода от функции 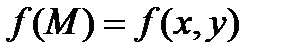 по кривой
по кривой 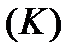 и обозначается:
и обозначается:
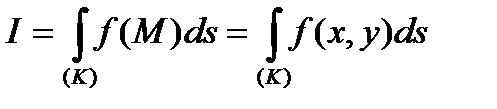 .
.
Тогда согласно формуле (20) и определению 1 масса кривой вычисляется как
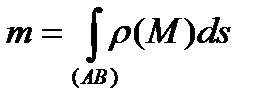 .
.
Замечание 1. В определении криволинейного интеграла І рода не имеет значения направление, которое выбирается на кривой  , т.е., если точки
, т.е., если точки  - это концы кривой
- это концы кривой  , то
, то
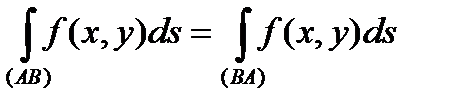 .
.
Аналогично определяется криволинейный интеграл І рода по кривой 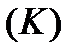 , которая находится не на плоскости, а в трехмерном пространстве:
, которая находится не на плоскости, а в трехмерном пространстве:
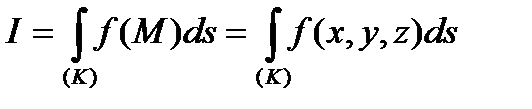 .
.
Дата добавления: 2015-08-21; просмотров: 650;
