Градиент функции
В каждой точке области D, в которой задана функция 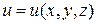 , определим вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке:
, определим вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке:
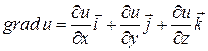
Этот вектор называется градиентом функции 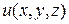 . Говорят, что в области D определено векторное поле градиентов. Докажем следующую теорему, устанавливающую связь между градиентом и производной по направлению.
. Говорят, что в области D определено векторное поле градиентов. Докажем следующую теорему, устанавливающую связь между градиентом и производной по направлению.
Теорема. Пусть дано скалярное поле 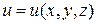 и определено в этом скалярном поле поле градиентов
и определено в этом скалярном поле поле градиентов 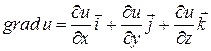 .
.
Тогда производная 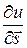 по направлению некоторого вектора
по направлению некоторого вектора 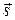 равняется проекции вектора
равняется проекции вектора 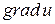 на вектор
на вектор 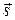 .
.
Доказательство. Рассмотрим единичный вектор 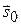 , соответствующий вектору
, соответствующий вектору 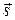 :
:
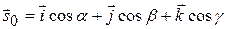 .
.
Вычислим скалярное произведение векторов 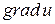 и
и 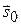 :
:
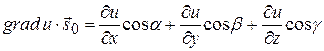 .
.
Выражение, стоящее в правой части этого равенства, есть производная от функции 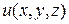 по направлению вектора
по направлению вектора 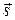 . Следовательно, справедливо
. Следовательно, справедливо
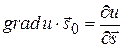 .
.
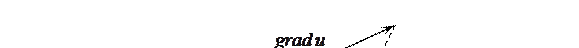
Если обозначим угол между векторами 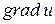 и
и 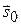 через
через 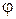 ,то можем написать:
,то можем написать:
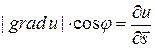 или
или 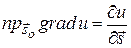 .
.
Теорема доказана.
На основании доказанной теоремы наглядно устанавливается связь между градиентом и производной в данной точке по любому направлению. Установим некоторые свойства градиента:
1) Производная в данной точке по направлению вектора 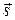 имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора 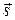 совпадает с направлением градиента; это наибольшее значение производной равно
совпадает с направлением градиента; это наибольшее значение производной равно 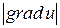 .
.
2) Производная по направлению вектора, перпендикулярного к вектору 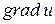 , равна нулю.
, равна нулю.
Замечание. Если функция 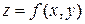 есть функция двух переменных, то вектор
есть функция двух переменных, то вектор
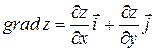
направлен перпендикулярно к линии уровня 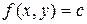 , лежащей в плоскости
, лежащей в плоскости 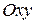 и проходящей через соответствующую точку.
и проходящей через соответствующую точку.
Пример. Определить градиент функции 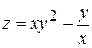 в точке
в точке 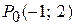 .
.
Решение.Частные производные
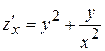 ,
, 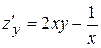
в точке 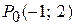 будут равны
будут равны
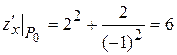 ,
, 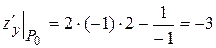 .
.
Следовательно,
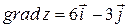 .
.
Дата добавления: 2015-08-21; просмотров: 1292;
