Производная по направлению. Рассмотрим в области D функцию и точку
Рассмотрим в области D функцию 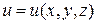 и точку
и точку 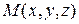 . Проведем из точки
. Проведем из точки 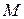 вектор
вектор 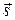 , направляющие косинусы которого
, направляющие косинусы которого 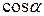 ,
, 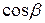 и
и 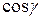 . Ha векторе
. Ha векторе 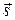 , на расстоянии
, на расстоянии  от его начала, рассмотрим точку
от его начала, рассмотрим точку 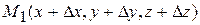 .
.

Длина вектора 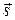 равна:
равна: 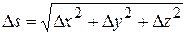 .
.
Будем предполагать, что функция 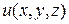 непрерывна и имеет непрерывные производные по своим аргументам в области D. В этом случае ее полное приращение представимо в виде:
непрерывна и имеет непрерывные производные по своим аргументам в области D. В этом случае ее полное приращение представимо в виде:
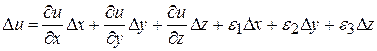 , (1)
, (1)
где 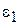 ,
, 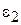 и
и 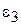 стремятся к нулю при
стремятся к нулю при 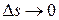 . Разделим все члены равенства (1) на
. Разделим все члены равенства (1) на 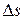 :
:
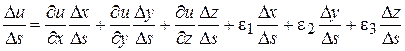 .
.
Очевидно, что 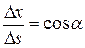 ,
, 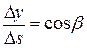 ,
, 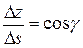 .
.
Следовательно, равенство (1) можно переписать так:
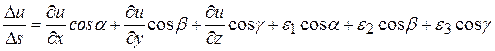 . (2)
. (2)
Определение. Предел отношения 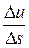 при
при 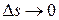 называется производной от функции
называется производной от функции 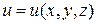 в точке
в точке 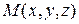 по направлению вектора
по направлению вектора 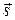 и обозначается
и обозначается 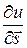 , т. е.
, т. е.  .
.
Таким образом, переходя к пределу в равенстве (2), получим:
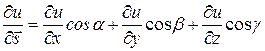 .
.
Величина 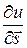 характеризует скорость изменения функции
характеризует скорость изменения функции 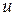 в точке
в точке  по выбранному направлению
по выбранному направлению 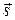 . Если
. Если 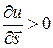 , то функция
, то функция 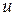 в точке
в точке  по направлению
по направлению 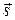 возрастает, в противном случае – убывает.
возрастает, в противном случае – убывает.
Отметим, что для функции двух переменных 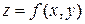 производная по направлению будет равна
производная по направлению будет равна
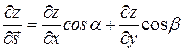 .
.
Пример. Найти производную функции 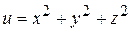 в точке
в точке 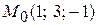 в направлении вектора
в направлении вектора 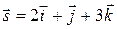 .
.
Решение. Найдем направляющие косинусы вектора 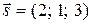 :
:
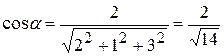 ,
, 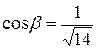 ,
, 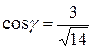 .
.
Частные производные 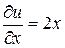 ,
, 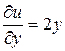 ,
, 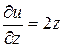
в точке 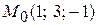 будут
будут 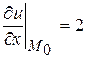 ,
, 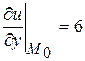 ,
, 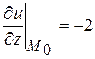 .
.
Следовательно, 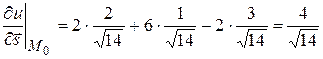 .
.
Пример. Найти производную функции 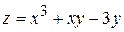 в точке
в точке 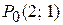 по направлению вектора
по направлению вектора 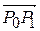 , если точка
, если точка 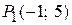 .
.
Решение. Вектор 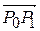 имеет координаты:
имеет координаты: 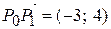 , длина вектора
, длина вектора 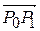 равна:
равна: 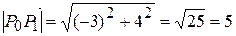 .
.
Найдем направляющие косинусы вектора 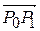 :
:
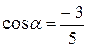 ,
, 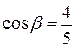 .
.
Частные производные 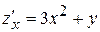 ,
, 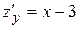
 .
.
в точке 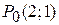 будут
будут 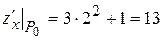 ,
, 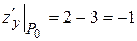 .
.
Следовательно, 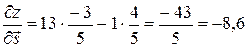 .
.
Дата добавления: 2015-08-21; просмотров: 662;
