Дифференцирование функции, заданной неявно
Известно, что функция 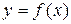 может быть задана неявно уравнением, связывающим переменные
может быть задана неявно уравнением, связывающим переменные 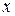 и
и 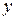 :
:
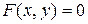 .
.
Например, уравнение 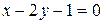 определяет функцию
определяет функцию 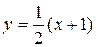 , при этом D
, при этом D 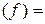 E
E 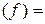 R.
R.
Уравнение 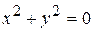 выполняется только при
выполняется только при 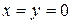 и задает точку
и задает точку 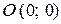 . Уравнение
. Уравнение 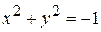 не определяет никакой функции на R,так как оно не имеет действительных корней, а значит, нельзя рассматривать
не определяет никакой функции на R,так как оно не имеет действительных корней, а значит, нельзя рассматривать 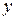 как функцию от
как функцию от 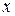 . Итак, уравнение вида
. Итак, уравнение вида 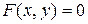 не всегда задает функцию
не всегда задает функцию 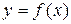 .
.
Пусть уравнение 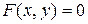 определяет
определяет 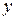 как некоторую функцию от
как некоторую функцию от 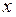 . Если в это уравнение подставить вместо у функцию
. Если в это уравнение подставить вместо у функцию 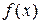 , то получим тождество
, то получим тождество
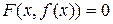 .
.
Придадим 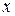 приращение
приращение 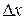 , тогда значению аргумента будет соответствовать значение функции
, тогда значению аргумента будет соответствовать значение функции 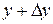 , но с другой стороны
, но с другой стороны
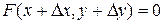 .
.
Разность 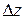 также равна нулю:
также равна нулю:
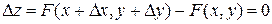 .
.
Как было показано выше, ее полное приращение в этой точке можно представить в виде
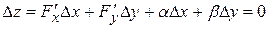 .
.
Разделим последнее равенство на 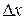 :
:
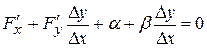 .
.
Откуда
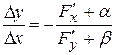 .
.
Перейдя к пределу, получим формулу вычисления производной функции, заданной неявно:
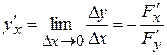 .
.
Аналогично можно вычислить частные производные неявной функции 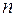 переменных по всем ее аргументам.
переменных по всем ее аргументам.
Например, для функции 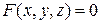 справедливо:
справедливо:
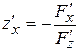 ,
, 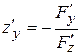 .
.
Пример.Вычислить производную неявной функции, заданной уравнением 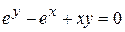 .
.
Решение. Обозначим левую часть данного уравнения через 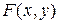 .
.
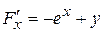 ,
, 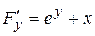 .
.
Следовательно,
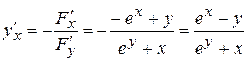 .
.
Пример.Вычислить производную неявной функции, заданной уравнением 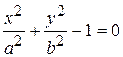 .
.
Решение. Обозначим левую часть данного уравнения через 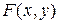 .
.
 ,
, 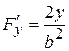 .
.
Следовательно,
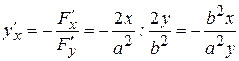 .
.
Пример.Найти частные производные неявной функции 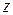 , заданной уравнением
, заданной уравнением 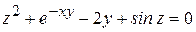 .
.
Решение. 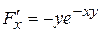 ,
, 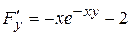 ,
, 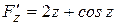 . Следовательно,
. Следовательно,
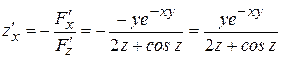 ,
,
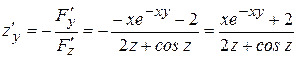 .
.
Дата добавления: 2015-08-21; просмотров: 980;
