Факторы, влияющие на интенсивность рентгеновского луча

Интенсивность определяется как квадрат структурной амплитуды:

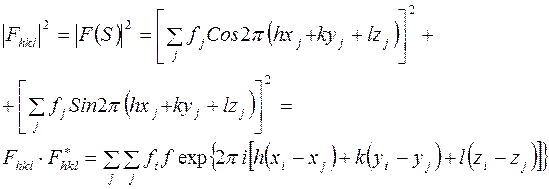. (1)

При известных координатах атомов рассчитать структурную амплитуду и интенсивность сравнительно просто. Но на практике приходится решать обратную задачу, т.е от структурных амплитуд требуется перейти к координатам атома. Из эксперимента можно определить лишь структурный фактор 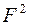или 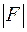, фаза структурной амплитуды 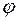- аргумент комплексного числа - может быть определена только в том случае, когда известна действительная ( 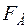) и мнимая ( 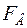) части структурной амплитуды:

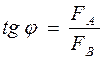. (2)

Учитывая, что 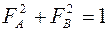, можно легко перейти к 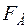и 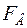, если известны 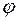и .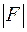

Чтобы решить конкретную структурную задачу, нужно в каждом отдельном случае универсальную формулу переводить в рабочий вид. Наличие элементов симметрии оказывает значительное влияние на расчетную формулу структурной амплитуды. Рабочие формулы структурной амплитуды строго индивидуальны для каждого класса Федоровской группы. Все они собраны в специальные справочники по рентгеноструктурному анализу.

Дифракционные спектры, из которых определяются интенсивности отражений, могут быть получены в различных устройствах (рентгеновских камерах, гониометрах, дифрактометрах), в которых пути прохождения падающего и отраженного пучка в веществе, а, следовательно, и результат взаимодействия с веществом различен. Это обстоятельство в первую очередь скажется на распределение интенсивности отражений.

Влияющие на интенсивность отражений факторы условно можно разделить на геометрические и физические.

Фактор поляризации.

Из теории рассеяния Х-лучей свободным электроном следует, что рассеянная волна не является сферически симметричной. Поэтому появляется множитель 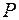, зависящий от угла .

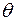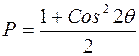, (3)

называемый фактором поляризации.

Если рассматривается конкретный метод исследования, то формула фактора поляризации имеет свой специфический вид (Хейкер, Зевин «Рентгеновская дифрактометрия»).

Фактор Лоренца

Если на сферу Эвальда выходит точка (а не конечная область), то рассеянный луч по теории должен быть бесконечно тонкич. Но Х-рефлекс имеет всегда какую-то вполне конечную ширину. Интенсивность в пределах рефлекса не одинакова. В рентгеноструктурном анализе интенсивность определяется максимальной высотой рефлекса, которая, конечно, не является отражением полной интенсивности рефлекса. Чтобы учесть всю интенсивность, вводится специальный множитель, позволяющий прейти от максимальной интенсивности к интегральной (фактор Лоренца).Так как форма Х-рефлекса достаточно хорошо описывается функцией Гаусса, этот фактор одинаков для всех методов и определяется соотношением:

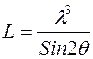(4)

(фактор Лоренца или кинематический фактор).

Геометрический фактор

Если рентгеновский луч встречается с регистрирующей пленкой под прямым или произвольными косыми углами, то форма и максимальная интенсивность рефлекса в этих двух случаях будут различны. Т.е. геометрические характеристики выбранной экспериментальной методики должны учитываться в формуле интенсивности. Для этих целей вводится специальный множитель ( ), называемый геометрическим фактором.

Итак, можно записать, что формула интенсивности рассеянного на кристалле рентгеновского луча будет иметь вид:

, (5)

где 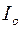- интенсивность первичного (падающего) пучка;

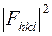- структурный фактор, учитывающий особенности строения решетки кристалла;

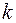- множитель, зависящий от физических свойств кристалла;

- произведение трех выше перечисленных факторов.

Для метода Дебая-Шеррера величина рассчитывается по формуле

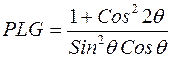. (6)

При регистрации спектра на плоскую пленку

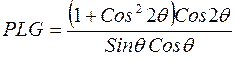. (7)

Для отражений от монокристалла

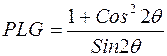. (8)

Если рентгенограмма получена в монохроматизированном излучении, а монохроматизация осуществляется кристаллом с углом отражения 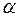, то

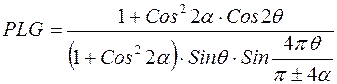(9)

Кроме факторов 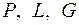, определяемых геометрией регистрации рентгенограмм, в формулу (5) входит множитель 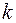, зависящий от физических свойств объекта исследования.

Рассмотрим некоторые.

Фактор повторяемости ( )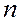

Из теории рассеяния Х-лучей на атоме следует, что с увеличением угла рассеяния интенсивность рассеянных лучей уменьшается. Если рассматривать картину дифракции от кристалла, то можно убедиться, что в области больших углов могут располагаться весьма интенсивные отражения. Особенно существенно это проявляется на рентгенограммах поликристаллов.

Обратное пространство для поликристалла представляет собой совокупность концентрических сфер. Каждая сфера практически равномерно заполнена узлами обратной решетки, которые соответствуют одинаковым значениям радиуса-вектора обратного пространства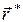

.

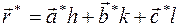Но одинаковое значение 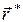, т.е. одинаковое 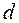, может быть у разных кристаллографических плоскостей. Например, у кубических кристаллов 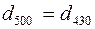. Кроме того, 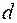одинаково для отражений .

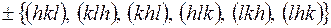Естественно, что плотность узлов на сфере обратного пространства, а, следовательно, и интенсивность отражений увеличится в 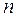раз, где 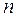- число плоскостей с одинаковым 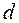. 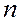есть фактор повторяемости.